[머신러닝] 결정 트리

[결정트리]

1. 결정트리의 원리

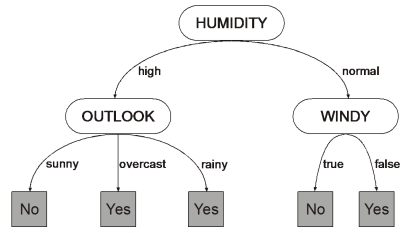
• 알고리즘 중 직관적으로 이해하기 쉬운 알고리즘
• 데이터에 있는 규칙을 학습을 통해 자동으로 찾아내 트리 기반의 분류 규칙을 만드는 것
• if/else 기반으로 자동으로 찾아내 예측을 위한 규칙을 만드는 알고리즘
• 데이터의 어떤 기준을 바탕으로 규칙을 만들어야 가장 효율적인 분류가 될 것인가가 알고리즘의 성능을 크게 좌우함
• 결정 트리의 구조 1) 규칙 노드: 규칙 조건이 됨 2) 리프 노드: 결정된 클래스 값 3) 서브 트리: 새로운 규칙 조건마다 생성됨 트리의 깊이가 길어질수록 과적합될 확률이 높아지고 결정 트리의 예측 성능이 저하될 가능성이 높음
• 가능한 적은 결정 노드로 높은 예측 정확도를 가지려면 데이터를 분류할 때 최대한 많은 데이터 세트가 해당 분류에 속할 수 있도록 결정 노드의 규칙이 정해져야 함
• 결정 노드는 정보 균일도가 높은 데이터 세트를 먼저 선택할 수 있도록 규칙 조건을 만듦, 정보 균일도가 데이터 세트로 쪼개질 수 있도록 조건을 찾아 서브 데이터 세트를 만들고, 다시 이 서브 데이터 세트에서 균일도가 높은 자식 데이터 세트를 쪼개는 방식으로 트리를 구성함
• 이러한 정보의 균일도를 측정하는 대표적인 방법은 엔트로피를 이용한 1) Information Gain 지수 와 2) 지니 계수가 있음

결정트리의 노드 분리의 기준

1) 엔트로피:

엔트로피는 주어진 데이터 집합의 혼잡도로 서로 다른 값이 섞여있으면 엔트로피가 높고, 서로 동일한 값으로 구성되어 있으면 엔트로피가 낮음. 이 엔트로피를 활용하여 정보이득(information gain) 계수와 지니 계수를 계산할 수 있음

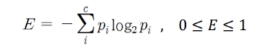
2) Information Gain: 엔트로피 개념을 기반으로 하며, 1-엔트로피 지수가 Information gain임. 이 지수가 높은 속성을 기준으로 활용하여 분할 기준을 정함

3) 지니계수: 경제학의 불평등 지수를 나타낼 때 사용하는 계수인데, 0이 가장 평등하고 1로 갈수록 불평등함, 머신러닝에서는 지니 계수가 낮을수록 데이터 균일도가 높은 것으로 해석하여 지니 계수가 낮은 속성을 기준으로 분할함

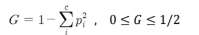
⇒ 이렇듯, Information gain가 높거나 지니 계수가 낮은 조건을 찾아 반복적으로 분할한 뒤, 데이터가 모두 특정 분류에 속하게 되면 분할을 멈추고 분류를 결정함

2. 결정 트리의 파라미터

1. min_samples_split : 노드를 분할하기 위한 최소한의 샘플 데이터 수로 과적합 제어에 사용됨, 작게 설정할수록 과적합 가능성 증가

2. min_samples_leaf: 말단 노드인 leaf가 되기 위한 최소한의 샘플 데이터 수, 과적합 제어에 사용되는데 imbalanced 데이터의 경우 특정 클래스의 데이터가 극히 작을 수 있어 작게 설정이 필요함

3. max_features: 최적의 분할을 위해 고려해야 할 최대 피처 수, 디폴트는 None이고 데이터 세트의 모든 피처를 사용해 분할을 수행함

4. max_depth : 트리의 최대 깊이를 규정, 디폴트는 None이며 완벽하게 클래스 결정 값이 될 때까지 깊이를 계속 키움

5. max_leaf_nodes : 말단 노드인 leaf의 최대 갯수

3. 결정 트리의 과적합

1) 결정 트리 하이퍼파라미터 디폴트 설정: iris 데이터를 사용하여 의사결정나무를 만들었을 때 트리 생성에 별도의 제약 없이 결정 트리의 하이퍼 파라미터를 디폴트로 한 경우, 일부 이상치 데이터까지 분류하기 위해 분할이 자주 일어나 결정 기준 경계가 많아짐, 디폴트 설정은 리프 노드 안에 데이터가 모두 균일하거나 하나만 존재해야하는 엄격한 분할 기준으로 인해 복잡해짐

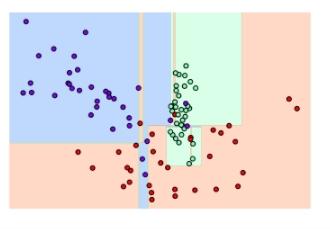
2) min_samples_leaf = 6으로 제한 조건을 건 경우 : 이상치에 크게 반응하지 않으며 general한 분류 규칙에 따라 분류됨

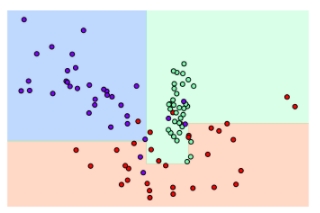
4. 결정 트리의 장단점

4-1. 결정 트리 장점

1. 쉽고 직관적임: 결정 트리 룰이 매우 명확하고, 어떻게 규칙 노드와 리프 노드가 만들어지는 지를 알 수 있고, 시각화로 표현할 수 있음

2. 변수처리가 쉬움: 정보의 균일도만 신경 쓰면 되므로 특별한 경우를 제외하고는 피처 스케일링과 정규화 같은 전처리 작업이 필요 없음

4-2. 결정 트리 단점

1) 과적합의 문제: 피처 정보의 균일도에 따른 룰 규칙으로 서브 트리를 계속 만들다 보면 피처가 많고 균일도가 다양하게 존재할수록 트리의 깊이가 커지고 복잡해져 과적합으로 인한 정확도가 떨어짐

2) 변수 상화작용 파악이 어려움: 한 번에 하나의 변수만을 고려하므로 변수간 상호작용을 파악하기 어려움

3) 선형 데이터에는 비적합: 결정경계(decision boundary)가 데이터 축에 수직이므로 특정 데이터에만 작동을 잘 할 수 있음

4) 에러 전파 : 계층적 구조로 인해 특정 노드에서 에러가 발생하면 다음 노드로 에러가 전파됨

5) 데이터에 영향을 받음 : 데이터의 변동과 노이즈에도 최종 결과가 크게 영향을 받음

6) 노드 갯수 갯수가 높아지면 오버피팅의 위험 : 낮은 bias, 높은 variance

과적합의 경우 ⇒ 모든 데이터의 케이스를 만족하는 완벽한 규칙은 만들수 없으므로, 트리의 크기를 사전에 제한하는 것이 성능 개선에 도움이 됨

오버피팅/과적합의 단점은 앙상블 기법에서는 장점으로 작용하는데 앙상블의 경우, 여러 약한 학습기를 결합해 확률적으로 보완하고, 오류가 발생한 부분에 대해 가중치를 계속 업데이트하며 예측 성능을 향상시키며, 이때 결정 트리가 좋은 약한 학습기가 됨

5. 결정트리의 종류

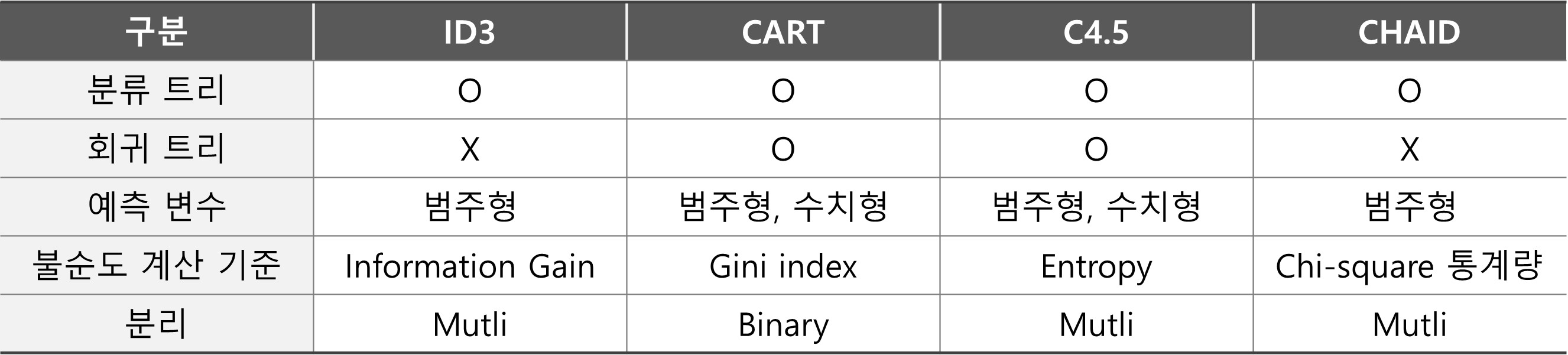
• 결정트리의 경우, ID3, C4.5, C5.0,CART, CHAID으로 알고리즘이 구분됩니다.

1) ID3, C4.5, C5.0 : 인공지능과 기계학습 분야에서 개발 및 발전되어 엔트로피와 정보이득을 활용

2) CART, CHAID : 통계학 분야에서 발전하여 카이제곱, T검정, F검정 등 통계량 활용

[결정트리 알고리즘에 따른 특징 정리]

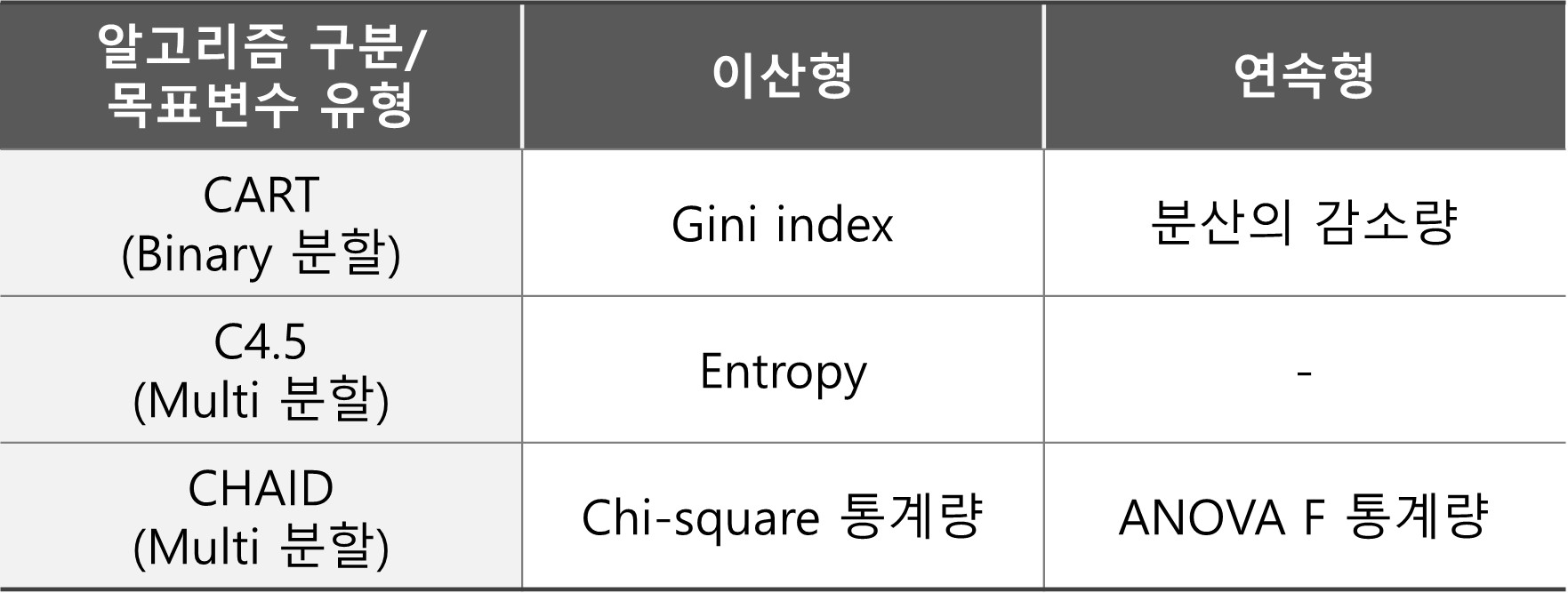
[목표 변수 유형에 따른 불순도 계산 기준]

후속으로 결정 트리의 상세 알고리즘에 대해 다뤄보겠습니다.

---

reference

파이썬 머신러닝 완벽가이드