[머신러닝] 회귀분석

회귀분석

[회귀분석]

1.회귀의 개념

• 회귀는 여러 개의 독립변수와 한 개의 종속변수 간의 상관관계를 모델링하는 기법을 통칭
• 머신러닝 회귀 예측의 핵심은 주어진 피처와 결정 값 데이터 기반에서 학습을 통해 최적의 회귀 계수를 찾아내는 것
• 회귀는 회귀 계수의 선형/비선형 여부(선형,비선형회귀), 독립변수(단일 회귀, 다중회귀)와 종속변수 개수에 따라 여러 가지 유형으로 나뉨
• 지도학습에서 예측값이 카테고리면 분류, 숫자값이면 회귀

2.선형회귀의 개념

• 선형회귀는 실제 값과 예측값의 차이(오류의 제곱값)를 최소화하는 직선형 회귀선을 최적화하는 방식임
• 선형 회귀는 규제(regularization) 방법에 따라 유형이 나뉨
• 규제(regularization) : 일반적인 선형 회귀의 과적합 문제를 해결하기 위해 회귀 계수에 페널티 값을 적용하는 것을 의미함 1) 일반 선형 회귀: 예측값과 실제값의 RSS(Residual sum of squares)를 최소화할 수 있도록 회귀계수를 최적화하며, 규제(regularization)를 적용하지 않은 모델 2) 릿지(Ridge): 릿지 회귀는 선형 회귀에 L2 규제를 추가한 회귀 모델임, 릿지 회귀는 L2 규제를 적용하는데 L2 규제는 상대적으로 큰 회귀 계수 값의 예측 영향도를 감소시키기 위해 회귀 계수값을 더 작게 만드는 규제 모델 3) 라쏘(Lasso): 라쏘 회귀는 선형 회귀에 L1 규제를 적용한 방식으로 L2 규제가 회귀 계수 값의 크기를 줄이는데 반해 L1 규제는 예측 영향력이 작은 피처의 회귀 계수를 0으로 만들어 회귀 예측시 피처가 선택되지 않게 만들고 이를 통해 피처 선택이 가능함 4) 엘라스틱넷(ElasticNet): L1,L2 규제를 결합한 모델이며, 주로 피처가 많은 데이터 세트에서 적용되며 L1 규제로 피처의 개수를 줄임과 동시에 L2 규제로 계수 값의 크기를 조정함 5) 로지스틱 회귀: 분류에 사용되는 선형 모델

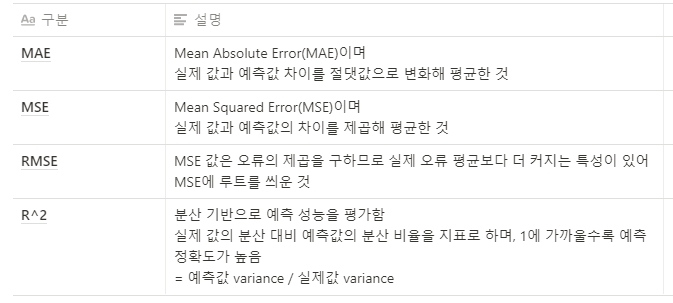
3. 회귀 평가 지표

• 회귀의 평가를 위한 지표는 실제 값과 예측값 차이 값을 기반으로 만든 지표가 중심 지표
• 오류의 절대값 평균이나 제곱, 제곱한 뒤 루트를 씌운 평균값을 구함

4. 규제 선형 모델

4-0. Regularization(규제)

• 회귀모델이 과소적합 또는 과대적합이 되지 않도록 데이터에 적합하면서도 회귀 계수가 커지는 것을 제어하는 점이 필요함
• 기본 선형 모델은 RSS(실제값, 예측값 간의 차이)를 최소화하는 부분만 고려하여 학습 데이터에 맞추려고 하고 이로 인해 회귀 계수가 쉽게 커짐, 이런 경우 변동성이 커져 테스트 셋에서는 예측 성능이 낮게 나올 수 있음
• 이를 방지하기 위해서는 RSS 최소화 방법과 과적합을 방지하기 위한 방법이 균형을 맞춰야 함
• 이를 위해 계수를 축소 : RSS + f(x)(회귀계수를 축소하는 항)

4-1. 릿지

• RSS최소화 방법 + tuning parameter * 회귀계수의 제곱의 합(과적합방지)
• tuning parameter를 크게 하면 비용 함수는 회귀 계수 값을 작게 하여 과적합을 개선하고 반대로 작게하면 회귀계수의 값이 커져도 상쇄가 가능
• tuning parameter를 사용하여 패널티를 부여해 회귀 계수 값의 크기를 감소시켜 과적합을 개선하는 방식을 Regularization(규제)이라고 부름
• 이러한 규제는 L1, L2로 구분됨. 릿지에서 사용되는 규제는 L2, L1은 회귀계수의 절대값에 패널티를 부여함. L2는 회귀계수를 0으로 만들지 않지만 L1은 0으로 만들 수 있음

4-2. 라쏘

• 회귀계수의 절대값에 패널티를 부여하는 L1 규제를 선형 회귀에 적용한 것
• L1 규제는 불필요한 회귀 계수를 0으로 만들고 제거함, 이를 통해 변수 선택 효과가 있음

4-3. 엘라스틱넷 회귀

• L1규제와 L2 규제를 결합한 회귀
• 엘라스틱넷은 라쏘가 서로 상관관계가 높은 피처의 경우 중요 피처만 선택하고 다른 피처들의 회귀계수는 0으로 만드는 성향이 강해 tuning parameter에 따라 회귀 계수의 값이 크게 변동할 수 있는 점을 보완하기 위해 L2규제를 추가한 것임
• L1, L2 규제를 모두 사용하여 수행시간이 상대적으로 오래 걸림

5. 선형회귀에 필요한 데이터 변환

• 데이터의 정규화와 인코딩 방법이 중요한 모델임
• 선형 모델은 피처와 타겟값 간 선형 관계가 있고, 이 둘의 분포가 정규 분포 형태를 가정하고 최적의 선형함수를 찾아낸 결과 값을 예측하는데 타겟값이 Skew (치우친) 분포일 때 예측 성능에 부정적인 영향을 줄 수 있음
• 이로 인해 선형 회귀 모델 사용 시에는 데이터가 지나치게 치우친 분포일 때 스케일링 및 정규화 작업을 수행함
• 스케일링: StandardScaler(평균 0, 분산1의 표준 정규분포), MinMaxScaler(최소값 0, 최대값 1 값으로 정규화)
• 로그 변환: log 함수를 적용하면 정규 분포에 가까운 형태로 값이 분포되는 경우가 있음, 타겟값의 경우 일반적으로 로그 변환을 적용함(치우친 분포의 타겟값을 로그 변환하여 성능 향상 사례가 많음)

6. 로지스틱 회귀분석

• 분류에 선형 회귀방식을 적용한 알고리즘
• 선형 회귀와의 차이점: 선형 함수의 회귀 최적선을 찾는 것이 아닌 시그모이드 함수 최적선을 찾고 이 시그모이드 함수의 반환 값을 확률로 간주해 확률에 따라 분류를 결정함
• 선형 회귀방식을 이용하되 시그모이드 함수를 이용해 분류를 수행하는 회귀임
• 시그모이드 함수의 y 값은 항상 0~1 사이의 값으로 x 값이 커지면 1에 가까워지고, x 값이 작아지면 0에 근사함, x가 0일 때는 0.5 시그모이드 이미지!!!!!!!!!!!

7. 회귀 트리

• 회귀 함수가 아닌 트리를 기반으로 하는 회귀방식
• 회귀를 위한 트리를 생성하고 회귀 예측을 하는 방법
• 분류 트리가 특정 클래스 레이블을 결정하는 것과 달리 회귀 트리는 리프 노드에 속한 데이터 값의 평균값을 구해 회귀 예측값을 계산함
• 모든 트리 기반 알고리즘(의사결정나무, 랜덤포레스트, GBM, XGboost, LighteGBM)은 분류 뿐 아니라 회귀도 가능함
• 선형회귀와의 차이점: 선형 회귀는 직선으로 예측 회귀선을 표현하는데 회귀 트리는 분할되는 데이터 지점에 따라 브랜치를 만들며 계단 형태로 회귀선을 만듦

8. 더 나아가서

• 스태킹 모델을 회귀에 적용도 가능함

reference

파이썬 머신러닝 완벽가이드