[머신러닝] SVM

[SVM(서포트 벡터 머신)]

• SVM은 선형, 비선형 분류, 회귀, 이상치 탐색에도 사용 가능한 다목적 머신러닝 모델이며, 복잡한 분류 문제에 잘 들어맞으며 작거나 중간 크기의 데이터셋에 적합함
• 분류 쪽의 성능이 뛰어나 주로 분류에 많이 활용되며, Hyperplane을 이용해 카테고리를 나눔

1. SVM 개요

1-1. 용어 개념

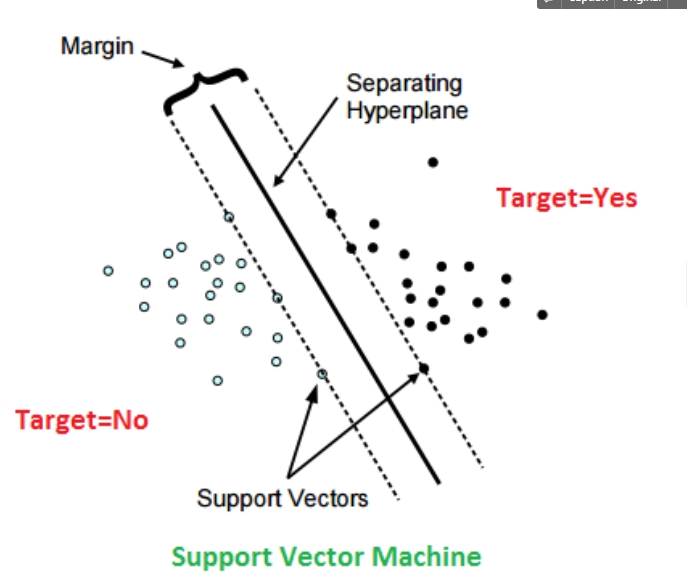
1) hyperplane : 다른 클래스 레이블을 가진 지정된 데이터 점 집합 사이를 구분하는 결정 경계, SVM은 최대 마진이 있는 hyperplane을 사용하여 사용하여 데이터 지점을 구분함, hyperplane의 dimension은 입력 변수의 변수 개수에 의해 정해짐(변수갯수-1) 2) support vector : 샘플 데이터 점으로 hyperplane에 가장 가까운 데이터 포인트이며, hyperplane의 위치와 방향에 영향을 줌

3) margin : margin은 가장 가까운 데이터 점에 있는 두 선 사이의 간격임. 즉, 서포트 벡터와 hyperplane 사이의 거리임, 이 값은 벡터 또는 가장 가까운 데이터 점과 직선으로부터의 수직 거리로 계산됨. SVM에서는 이러한 분리 격차를 극대화하여 최대 margin을 달성하려고 함

1-2. SVM 원리

• SVM의 주요 목표는 주어진 데이터 셋의 support vector에 가능한 최대 margin이 있는 hyperplane을 선택하는 것, 두 클래스 간에 가장 큰 margin을 만들어내는 최적의 hyperplane 찾는 것

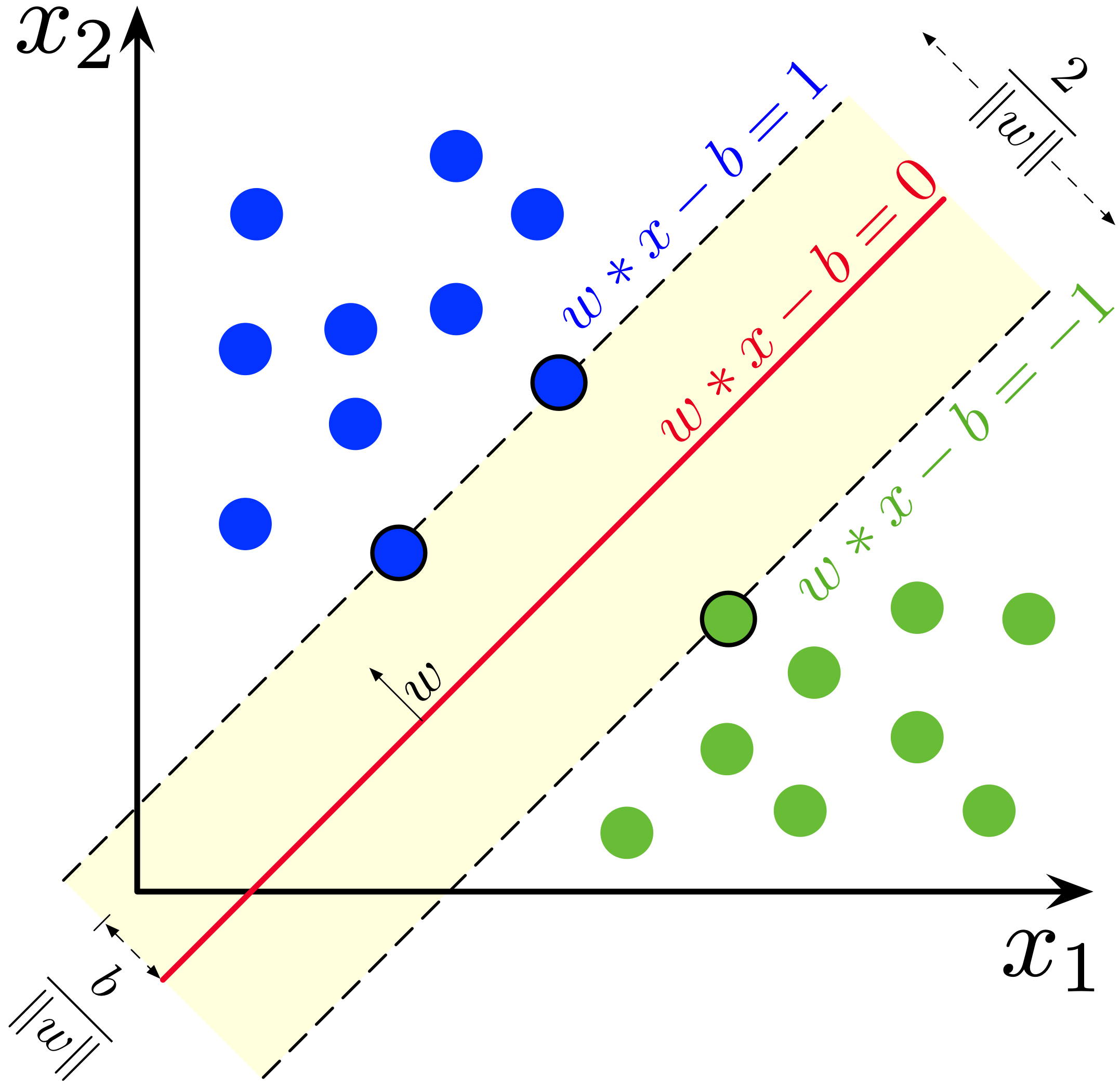
1-3. SVM의 수학적 개념

1) margin을 최대화하는 문제

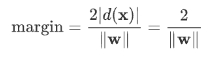
2) linear 제약조건

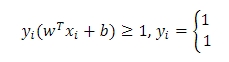
3) 제약조건을 만족시키며, margin을 최대화 하도록 w와 b를 찾아야 함

• Lagrange multiplier를 활용하여, 풀 수 있음

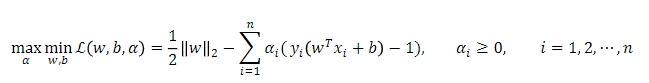
최소값을 찾기 위해 미분시 0이 되는 지점을 찾을 수 있고(convex optimization problem), hyperplane의 w와 b를 구할 수 있음

⇒ 결국, 최대 마진을 구하는 문제를 최소화하는 문제로 바꾸어 풂

Train set에서는 마진을 최대로 하는 hyperplane을 찾고(w와 b를 계산), test에서는 데이터가 결정경계의 위쪽인지, 아래 쪽인지 분류함

cf) Lagrange multiplier(라그랑주 승수)의 아이디어: 최소화 또는 최대화 하는 값을 찾고 싶을 때 f(x,y)를 최대화하는 동시에 g(x,y)=c로 한정하고 싶은 경우, f(x,y)와 g(x,y)가 접할 때 f(x,y)의 극대값 혹은 극소값이 만들어짐

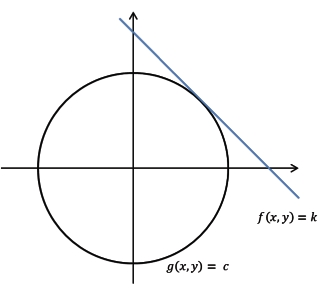
• 임의의 λ가 존재하여

\(\Delta f = \Lambda \Delta g\) 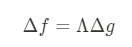가 만들어지는 지점에서 극대, 극소값이 발생하므로 g(x,y) = c 제약 하에서 f(x,y)를 최대화 하는 것은

L(x,y,λ)를 최대화하는 것과 같음 L(x,y,λ) = f(x,y)-λ(g(x,y)-c)

2. 선형 SVM 분류

• 마진과 학습 오류의 갯수는 trade off 관계가 있음

1-1. Cost에 따른 분류

• Slack 변수: 선형적으로 분류가 어려운 경우, 분류를 위해 오차를 허용할 때 사용하는 변수, 오버피팅 현상이 발생할 수 있어 고안된 개념

  

1) Slack 변수 = 0 : 정상적으로 분류된 경우

2) Slack 변수 > 0 또는 Slack 변수 = 1 : 마진이 적은 경우

3) Slack 변수 > 1 : 분류가 잘못 된 경우

• COST(regularization parameter): 오버피팅을 막기 위한 penalty항으로, 일반화 목적으로 들어가는 것, 다른 클래스에 놓이는 정도를 허용하는 것

  

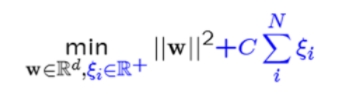
1) C 값이 큰 경우 : 허용 오차의 갯수가 작아야 하므로 W에 집중하여 margin이 좁아지는 경향이 있음, 허용 오차 갯수를 적게 허용하므로 세심한 결정 경계를 가짐, 정확하게 분류하지만 과대적합/오버피팅 가능성이 커지므로 새로운 데이터가 들어올 때 잘 분류할 수 없을 수도 있음

2) C 값이 작은 경우 : 허용 오차를 많이 허용하여 일반적인 결정경계를 가짐. 즉, margin이 커짐

⇒ C의 유무에 따라 하드마진 SVM과 소프트마진 SVM으로 나뉨

1-1. 하드 마진 분류

• 모든 샘플이 직선 바깥쪽에 올바르게 분류되어 있는 것
• 하드마진의 문제점

1) 데이터가 선형적으로 구분될 수 있어야 제대로 작동

2) 이상치에 민감

1-2. 소프트 마진 분류

• 하드 마진의 문제를 피하기 위해서는 유연한 모델이 필요함.

• 도로의 폭을 가능한 넓게 유지하는 것과 마진오류(샘플이 도로 중간에 있거나 반대쪽에 있는 것) 사이에 적절한 균형을 잡는 것을 소프트 마진 분류라고 함
• SVM 모델에서 C 하이퍼파라미터를 이용해 균형을 조절할 수 있음
• C를 줄이면 도로의 폭이 넓어지지만 마진 오류도 커짐
• SVM 모델이 과적합이면 C를 감소시켜 모델을 규제 할 수 있음

2. 비선형 SVM 분류 : 커널 SVM

• 선형 분류가 되지 않는 데이터셋에 비선형 SVM 분류를 적용
• 비선형 데이터셋을 다루는 방법은 다항 특성과 같은 특성을 더 추가하여 선형적으로 구분되는 데이터셋이 만들어질 수 있음

2-1. 커널에 대한 개념

• 선형 SVM으로 데이터를 제대로 분류할 수 없는 경우, 커널함수라는 매핑함수로 저차원 공간을 고차원 공간에 매핑

  

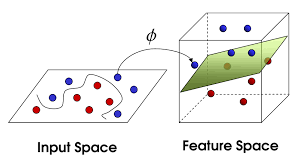
• 고차원으로 변환하는 경우, 계산이 많아지는데 커널 트릭의 경우 데이터를 실제로 고차원으로 보내지 않지만 동일한 효과를 주어 빠른 속도로 hyperplane을 찾을 수 있음

[커널의 종류]

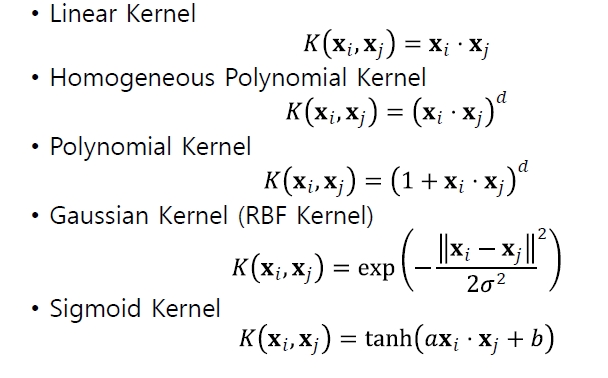
사용하는 kernel에 따라 feature space의 특징이 달라지므로, 데이터의 특성에 맞는 kernel을 결정하는 것이 필요하며, 일반적으로 RBF kernel, sigmoid kernel 등이 주로 사용됨

2-2. 다항식 커널

• 커널은 데이터를 분리할 수 있게 더 높은 차원으로 매핑하는 함수로 입력 공간을 고차원 공간으로 변환함. 따라서 더 많은 차원을 추가하여 비선형 문제를 선형 문제로 변환함
• 다항식 특성을 추가하는 것은 간단하고 모든 머신러닝 알고리즘에서 잘 작동하지만 낮은 차수의 다항식은 매우 복잡한 데이터셋을 잘 표현하지 못하고 높은 차수의 다항식은 굉장히 많은 특성을 추가하므로 모델을 느리게 만듦
• 인기 커널은 선형 커널, 폴리노미알 커널, 방사 기반 함수(RBF)커널, 시그모이드 커널 등이 있음
• SVM의 경우, 커널 트릭이라는 수학적 기교를 적용할 수 있음, 실제로 특성을 추가하지 않았지만 다항식 특성을 추가한 것과 같은 결과를 얻을 수 있음, 어떤 특성도 추가하지 않았으므로 엄청난 수의 특성 조합은 생기지 않음
• 커널을 사용하는 경우, 고차원을 잘 디자인해서 변형하고 이로 인해 inner product가 획기적으로 줄어듦

2-3. 유사도 특성 추가

• 각 샘플이 특정 랜드마크와 얼마나 닮았는지 측정하는 유사도 함수로 계산한 특성을 추가할 수 있음
• 가우시안 RBF를 활용하면 랜드마크에서 아주 멀리 떨어진 경우는 0으로, 같은 위치일 경우 1로 종 모양을 나타남
• 가우시안 RBF를 가지고 특성을 새로 만들 수 있으며, 이 특성들은 선형적으로 구분이 가능함
• 랜드마크는 데이터셋에 있는 모든 샘플 위치에 랜드마크를 설정하는 것으로 이렇게 하면 차원이 매우 커지고 따라서 변환된 훈련 세트가 선형적으로 구분될 가능성이 높다고함

2-4. 가우시안 RBF 커널

• 유사도 특성의 경우 모두 계산하려면 연산 비용이 많이 드는데 가우시안 RBF 커널을 적용하면 유사도 특성을 추가한 것과 같은 결과를 특성을 추가하지 않고 얻을 수 있음

3. SVM 회귀

• SVM 회귀는 일정한 마진 오류 안에서 두 클래스 간의 도로 폭이 가능한 최대가 되도록 하는 대신, SVM회귀는 제한 된 마진 오류(도로 밖의 샘플) 안에서 도로 안에 가능한 한 많은 샘플이 들어가도록 학습함

4. SVM의 장단점

4-1. SVM 장점

1) 오류 데이터의 영향이 적음

2) 과적합이 되는 경우가 적다

4-2. SVM 단점

1) 여러 개의 조합 테스트가 필요함

2) 학습 속도가 느림

3) 해석이 어렵고 복잡함

---

reference

• 핸즈온머신러닝(마스터알고리즘 추천)
• 쉽게 읽는 머신 러닝