[강화학습] Markov Decision Process

2. Markov Decision Process

1. Markov Processes

• Markov decision processes는 강화학습에서 evironment를 describe하며, 이때 environment는 fully observable 되는 상황으로 가정함
• current state가 the process를 완전히 characterises함
• 대부분의 RL 문제는 MDP로 공식화가 가능함(partially observable 문제도 MDP로 전환 가능)

2. Markov Property

Markov property

• 현재가 주어졌을 때 미래는 과거에 independent함

• S(1)~S(t)를 아는 것과 S(t)만 아는 것은 동일함

  ### State Transition Matrix

  

• state s와 다음에 오는 state s’의 state transition probability는 P(ss’)로 정의되고,
• state transition matrix P는 s → s’의 transition probabilities를 정의함

Markov Process

• 현재의 state만을 가지고 random process(확률적으로 시간 흐름에 따라 변화하는 구조)
• Markov Process = <S,P> state와 transition probabily
• S: finite set of states
• P: state transition probability matrix P(ss’)

MP example : student Markov Chain Episode

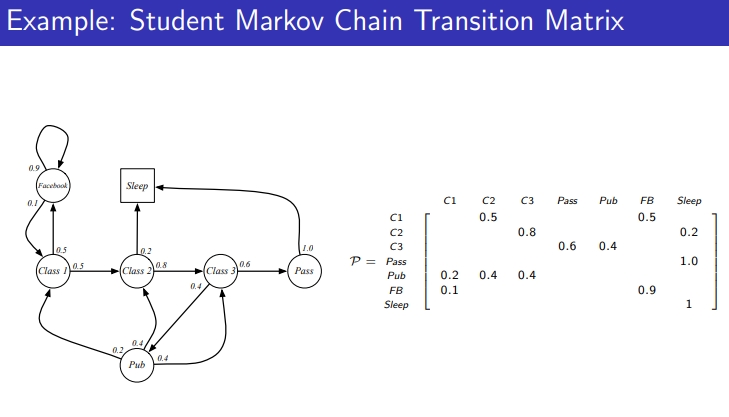
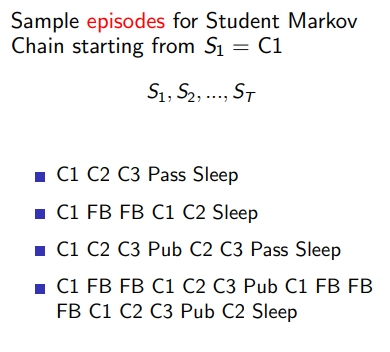
• P 행렬로 표현

3. MRP

3-1. MRP 의미

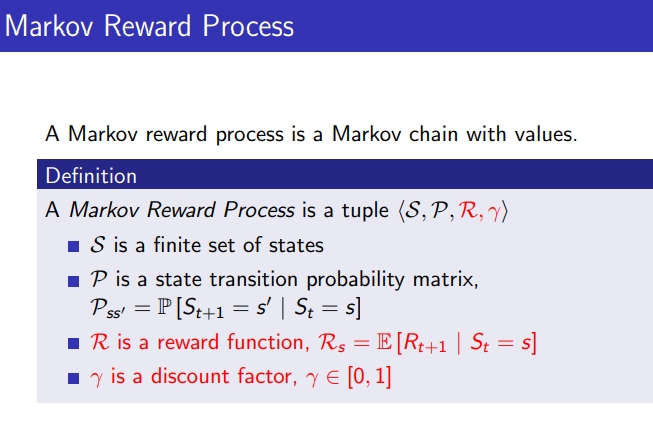
• MRP는 Markov Process에 reward가 추가된 것
• MRP = <S,P,R,Γ>
• S: finite set of states
• P: state transition probability matrix P(ss’)
• R: reward funtion
• Γ: discount factor

MRP example : student Markov Chain Episode

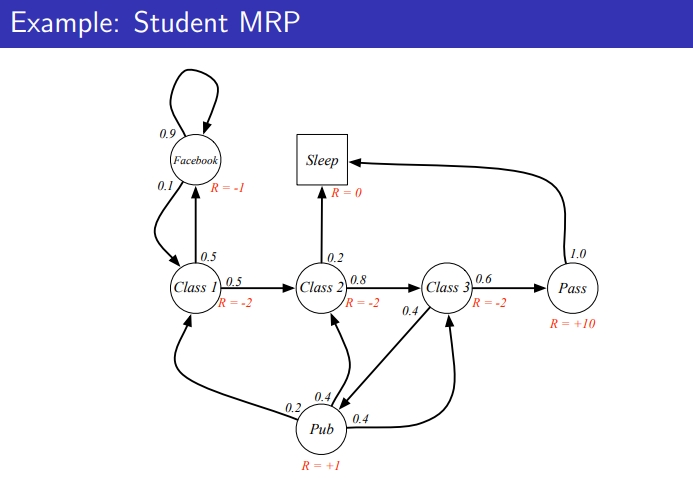
3-2. Return

• G(t) : time stept t의 total discounted return
• discount Γ: future rewards의 present value(t+2부터 discount factor을 곱함 Γ,Γ^2, Γ^3 ,… )
• Γ 0에 가까운 경우, 근시안적으로 지금의 state만을 중요시 여기는 평가 진행

• Γ 1에 가까우면 장기적인 관점의 평가를 함

  

• 대부분의 Markov reward와 decision process는 discounted 되는데 이유는?

1) avoid infinite return : step이 무한하게 발생하는 경우, 무한대로 갈 수 있는데 Γ를 이용해 discount해서 반영 exponentially reward가 낮아짐

2) 미래에 대한 불확실성이 fully represented되지않음

3) 현재 리워드에 더 가중치를 줌

• discount되지 않은 Γ=1인 경우도 있는데 toy example인 경우 1 가능

3-3. Value fucntion

• MRP의 Value function V(s) : state s에서 시작한 expected return

Example: Student MRP return

• r에 따라 value function은 달라짐

3-4. Bellman Equation

Bellman equation for MRPs

• Value funtion은 1) immediate reward R(t+1) 2) discounted value of successor state ΓV(S(t+1))으로 구성됨

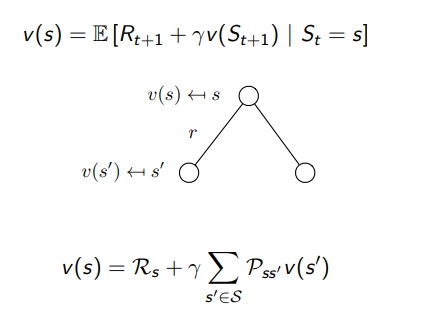
• v(s) = 즉각적인 리워드 + next state의 value fuction
• v(s’)에 transition probabilty를 곱해줌

Example: Bellman Equation for Student MRP

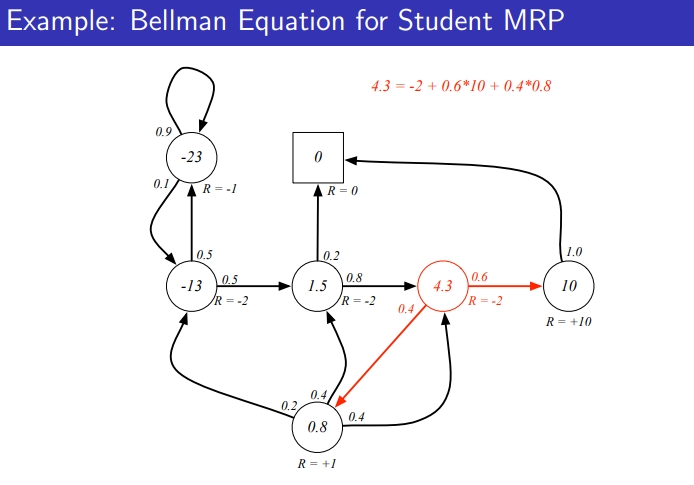
• v(s) 4.3 = -2 (즉각 리워드) + 0.6 * 10 + 0.4 + 0.4*0.8
• 모든 transition probabilty와 value function 곱해줌
• value function이 서로를 구하는데 영향을 계속 해서 주는데 이를 계속 반복하면 value function이 수렴하게 됨

요약: Bellman Equation은 즉각 리워드 + transition probabilty * 연결된 value function

Bellman Equation in Matrix Form

Solving the Bellman Equation

• n이 커지면 계산에 어려움이 있어서 MRP가 커지면 다이렉트하게 풀기보단 다이나믹 프로그래밍을 사용

4. Markov Decision Process

4-1. Markov Decision Process

• MDP는 MRP에 action 정보까지 들어간 것
• MDP = <S,A,P,R,Γ>
• S: finite set of states
• P: state transition probability matrix P(ss’)
• R: reward funtion
• Γ: discount factor
• A: finite set of actions
• P(a,ss’) : 어떤 Action을 했을 때, 어떤 State로 가는지 transition probability
• R(a,s) : 어떤 Action을 했을 때 어떤 Reward가 생기는지

Example: Student MDP

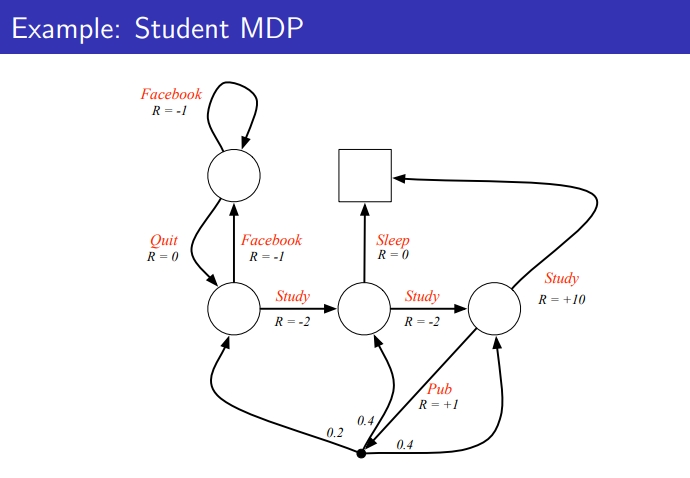
• MRP는 state에 도달하면 그 state에 대한 Reward가 주워짐
• MDP는 특정 Action했을 때 도달하고 Reward가 주워짐

4-2 policies

• policy: 어떤 state에서 어떤 Action을 할 확률
• policy는 agent의 behavior을 정의하고, MDP policies는 current state에 depend

• policy는 stationary : state가 동일하다면 state에 의해 Action하는 확률도 같아야 함

  

• P(π, s,s’) : 어떤 state에서 Action할 확률 * Action을 취했을 때 다른 State로 가는 transision prob. ⇒ transision prob과 policy가 맞물려서 결정됨
• R(π,s)

4-3. Value Function

• state-value : given policy π에 의해서, 주어진 State에서 끝까지 갔을 경우 return 값의 기댓값, state s에 대해 이 policy를 따르는 value 값
• action-value: given policy π에 의해서, 주어진 state에서 어떤 Action을 택했을 때 그 이후로부터 return 값의 기대값

4-4. Bellman Expectation Equation

• state value function: 즉시 발생 리워드 + 그 이후 state에서의 policy에 따른 value 값(discount)

• action value function: 즉시 발생 리워드 + 그 이후 state에서 policy에 따라 임의의 action 선택한 value 값(discount)

  ### 4-5. Bellman Expectation Equation for Vπ

  

• Vπ(s) : π에 따라 Action 선택
• Qπ(s): 어떤 State에서 π에 따라 어떤 Action 선택
• value function을 policy와 q함수 조합으로 재정의
• v를 q로 표현

4-6.Bellman Expectation Equation for Qπ

• q를 v로 표현
• qπ(s,a) = 즉각적으로 발생하는 리워드 기댓값 + 어떤 state에서 다른 state로 갈 확률 * 그 확률에 따라 그 state로 갔을 때의 value 값

References

Lecture 2: Markov Decision Processes