[강화학습] Model-based Planning

3. Model-based Planning (4강 model_based)

강의록4.model_based

1. Planning & Learning

• sequential decision making에서 2개의 fundamental problems이 있음

1-1. Planning

• Environment의 model(MDP)가 알려져 있고
• agent가 그 모델과 interaction
• agent가 policy를 improve

1-2. Learning

• envrionment을 모름
• agent가 environment와 interacts
• agent가 policy를 improve

1-3. 다이나믹 프로그래밍

• 복잡한 문제를 간단한 규모로 쪼개고 작게 만듦
• shortest path를 찾는 문제가 있다고 하면 전체 path를 모두 나열하긴 힘들기 때문에 각각의 쪼개서 각각의 short path를 구하고 원래 원했던 전체 path의 최소를 구함
• MDP는 다이나믹 프로그램밍에 필요한 요소들을 모두 만족

1-4. Planning by Dynamic Programming

• MDP에 대해 full knowlege있다고 가정

1) Prediction (evaluation)

• Input : MDP <S,A,P,R, Γ>, π
• output: value function Vπ

MDP와 policy에 따른 value function을 계산하는 것이 policy evaluation

2) Control (improvement)

• input: MDP
• output: optimal value function V* and optimal policy π*

랜덤 π에서 시작해서 그 π를 가지고 iterative하게 정정, π를 evaluation하고 그 결과로 π improve, 최종은 optimal policy & value function 구하기

2. Policy Evaluation & Policy Iteration & Improvement

2-1. Iterative policy evaluation

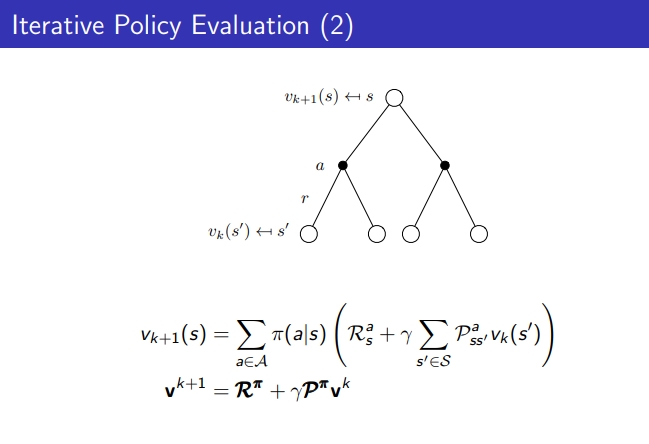
• policy를 evaluate하는 방법: bellman expectation backup(iterative하게 얻어내는 걸 backup이라고 함)
• 모든 value function을 initialize하고 Vk(s’)로 Vk+1(s)를 업데이트함(state의 value 값은 이전 값으로 만듦)
• k가 무한대로 간다면 Vπ를 따르는 value function을 구해낼 수 있다.

Example : Small Grid World

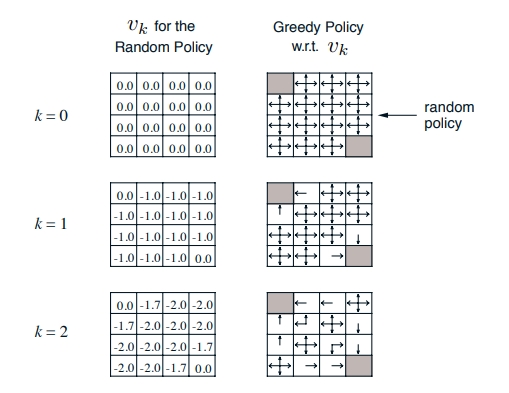
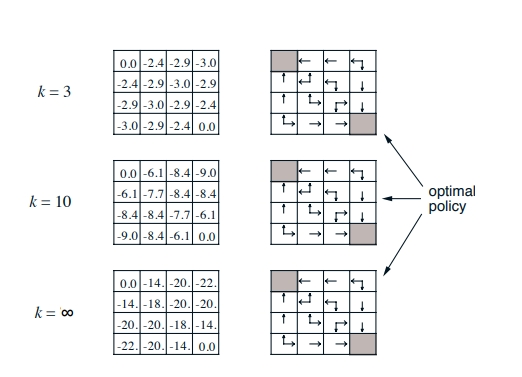
• π가 주어짐, policy의 value 값 어떻게 논할까, 0.25로 줌
• 처음에 v값을 initialize하게 0으로 줌
• 업데이트 하는 방법: 즉각 리워드 + 감마*발생할 수 있는 모든 next state value 값 *V(바로 이전 값)
• 1,2행을 구해보자면

1) UP: v(s) = 0.25 * (-1 +0) = policy * (즉각 리워드 + 이전 value 값)

2) DOWN, LEFT , RIGHT도 같은 방식으로

v(s) = 4 * 0.25 * -1

• k가 높아지면서 수렴됨

2-2. Iterative Policy Evaluation

• Input π, π는 evaluated
• 수렴하는 값에 대해 threshold θ를 줌
• V(s)를 initailze하고, 터미널 V 값을 0으로 둠
• 모든 state에 대해 현재 state의 value 값을 가지고 옴
• policy의 action마다 구하고 이전 iteration의 value값을 더 함
• V(s) 값이 갱신되는데 더 이상 변하지 않는 값이 옴, 각 state 중 가장 큰 값을 찾아 threshod와 비교

2-3. policy iteration

• policy evaluation과 improvement의 반복

주어진 policy에 대해

STEP1. policy를 evaluate함

STEP2. Vπ에 관해 greedy acting하면서 policy를 improve함

• Small grid world에서는 몇번 반복하면 policy가 optimal하지만 보통은 더 많은 반복이 필요함
• policy iteration은 항상 optimal policy에 도달함

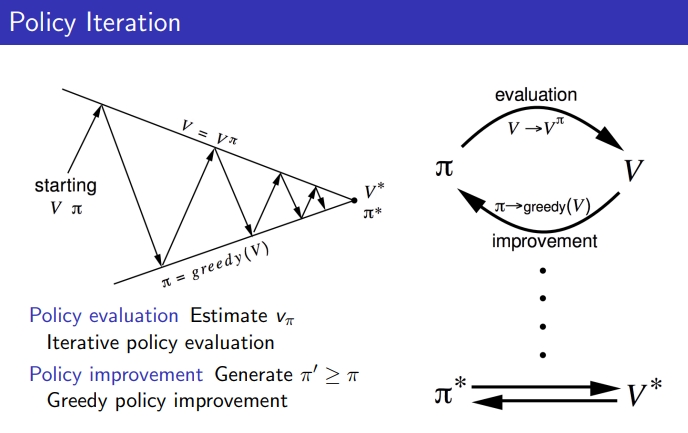
1) policy evaluation: 이 π에 대해 V가 수렴할 때까지 계속해서 evaluation함

2) Policy improvement: 수렴된 V를 가지고 policy를 update함, 그리고 새 π에 대해 수렴할 때까지 evaluation

1),2)의 과정을 반복하여 π와 V 모두 optimal한 상태가 됨

2-4. Policy Improvement

• greedy하게 improve된 policy에 의한 Q 값
• = 원래 policy로 할 수 있는 action의 max값

• ≥ 그 state에서 주어진 policy에 의해 action의 q값의 기댓값이 같아야함

  

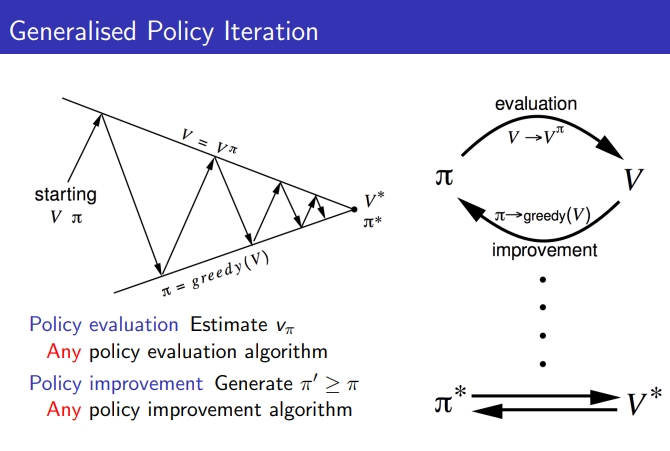
• general한 방법이 있음

1) k = ∞, greedy policy improvement 사용

2) k = 1, greedy 알고리즘 사용

1),2) 같이 사용

3. Value Iteration

3-1. Principle of Optimality

• optimal policy은 2개의 요소 나뉘어짐

1) optimal first action A

2) optimal policy from successor state S’

• S1 →(opt)→ S2 →(opt)→ S3 , S1 →(opt)→ S3도 opt을 구할 수 있다

3-2. Deterministic Value Iteration

• 어떤 state에서 즉각적인 리워드 얻었을 때 next state의 optimal 값을 안다면 현재 ~ 터미널까지 optimal 값을 계산할 수 있음

3-3. Value Iteration

• 벨만 optimal 상태인 걸로 가정하고 max를 가지고 옴

  

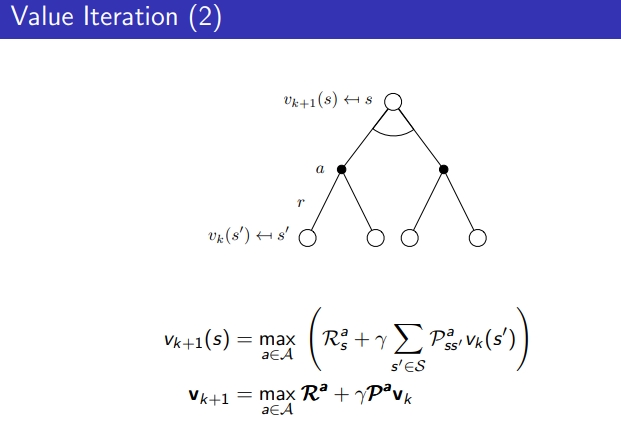
• 벨만 optimal을 K+1에 적용함 k번째 값으로부터
• policy iteration과는 다르게 evaluation과 improvement가 구분되어 있지 않음
• Action별 기댓값 중 max로 업데이트만 반영, Value값 변화 없으면 argmax 취해서 optimal policy를 얻음

4. Summary

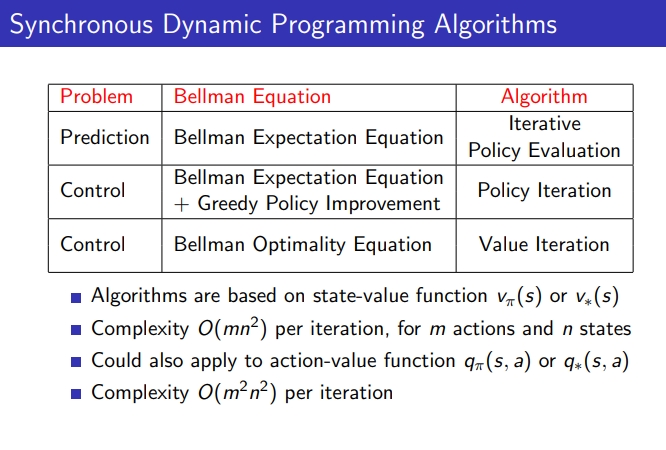
• Iterative Policy Evaluation : Bellman Expectation Equation → evaluation만 하고 싶은 경우
• Policy Iteration : Bellman Expectation Equation + Greedy Policy Improvement
• Value Iteration : Bellman Optimality Equation

과제 관련

References:

David Silver Lecture 3: Planning by Dynamic Programming