4. Model Free Prediction(5)

- 지금까지는 주어진 MDP를 활용하여 다이나믹 프로그래밍으로 주어진 MDP로 planning을하여 optimal policy를 얻음(policy iteration, value iteration)
- 그러나 MDP를 모르거나, MDP를 알아도 너무 커서 full backup이 어려운 경우(다이나믹 프로그래밍 다하기 힘든 경우) → Model Free prediction을 진행
1) model prediction(evaluation)
→ unkown MDP에 대해 value function을 estimate(지난 시간엔 MDP를 가지고 다이나믹 프로래밍하여 value funtion 계산)
→ 주어진 policy가 얼마나 좋은가
2) model free control(improvement)
→ unkown MDP에 대해 value funtion을 optimize하는 것
→ better policy를 어떻게 learn할 것인가
1. Monte-Carlo Reinforcement Learning
1-1. Monte-Carlo

1) 몬테 카를로 방식은 sampling으로부터 original을 추정하는 방식임, 랜덤 샘플링을 반복하고 original 형태를 알아내는게 MC
2) A class of computational algorithms that rely on repeated random sampling to obtain numerical results.
3) 샘플링이란 직접 경험으로부터 learn함
4) MDP의 transition과 reward를 모름
5) complete epsiode : S(시작)→T(끝)까지 끝까지 경험한 에피소드
6) No bootstraping: 벨만 expectation처럼 사전에 미리 구한 값을 재활용 불가 V(S(t)) = R + V(S(t+1))
7) simplest possible idea : value funiction = sampling한 return의 평균값
8) MDP를 알면 기댓값을 계산 가능, 모르면 샘플링을 통해 평균값을 얻을 수 있음
1-2. Monte-Carlo Learning

1) Goal: 주어진 policy로 에피소드를 수행 → 모든 state(경험을 통해 배운 애들만)의 value function 학습
2) Value function = expected return
1-3. First-Visit Monte-Carlo Policy Evaluation

- 5개의 state가 있다고 하자 S1(start) , S2 , S3 , S4 , S5(terminal)
- S1 S2 S1 S4 S5 → S1이 2번 출현 → first visit monte carlo N(s)에 대해 반복 출현 중 최초 등장한 한번만 카운트함
- Value = S(s)/N(s) : value는 mean return으로 estimate 가능
- Increment counter : N(s) ← N(s) + 1
- Increment total return: S(s) ← S(s) + G(t) → S5(terminal)까지에 대해서 S1,S2,S4에서 terminal까지의 G값 더함(각 State의 G값 더하기)
- (G(t) = discount total reward)
- 대수의 법칙에 의해, n이 무한대로 가면 state value 값이 수렴됨
1-4. Every-Visit Monte-Carlo Policy Evaluation

- Every-Visit Monte-Carlo Policy Evaluation은 여러 번 출현한 경우 모두 카운트를 해주는 것
1-5. Incremental Mean

- U(k) = (K)평균값 = (K-1)평균값 + (1/K)(샘플값K - (K-1)평균값)
- U(k): K번째 평균값은 K값 더해서 나눠줌의 평균
- 계속해서 이전 평균값과 알고 K번째만 알면 구할 수 있음
1-6. Incremental Monte-Carlo Updates

- increment mean 방법을 incremental monte carlo에서도 사용 가능
- V(S(t)) ← V(S(t)) + (1/N(S(t))(G(t)-V(S(t))
- 새로 얻은 G - 이전까지 알고 있던 value 값에 1/N 반영
- 1/N을 α로 constant한 hyper parameter로 반영하기도 함 1) 과거 데이터를 잊어버리고 새로 습득하는 G값을 계속 반영 2) n이 작을땐 처음엔 크게 반영하여 이를 방지하기 위해 사용
- incrementally 평균값 유지 → N이 커질 때 기댓값으로 근사되는데 N이 너무 커지면 차의 반영이 퇴색됨 → 수렴 안됐는데 그렇다면 또는 업뎃 된걸 안되면 α로 넣어줌 → 일종의 learning rate
[요약]
- Policy를 모르는데 MDP를 안다면 → learning 아닌 planning 개념으로 다이나믹 기법으로 policy를 evaluation 가능
- Policy가 주어졌는데 MDP를 모르면 → 어떻게 Policy를 eval & prediction할 수 있을까? → Model Free 사용
- 몬테카를로를 사용하는 것은 Model인 MDP를 모르는 상황에서 policy가 주어졌을 때 evaluation & prediction을 하기 위함임
- 몬테카를로는 직접 샘플링으로 Value Function을 점진적으로 업데이트함 → 어떤 환경에 대해 주어진 Policy로 실제 action을 수행하고 그때 경험된 state와 reward 값으로 각 state의 값을 update 해나감 → 각 State의 terminal 갔을 때의 return인 G를 더해주고 n으로 나눈 평균 → N이 충분히 커지면 평균값이 기댓값에 근사함 → incremental하게도 가능함 → 이번에 얻은 기댓값-직전 알고 있던 평균값 → 그 차를 1/n만큼해서 더해줌
2. Temporal-Difference Learning

- 몬테카를로와 같이 TD를 사용하여 pratical하게 경험으로부터 얻음
- TD도 MC와 같이 1) episode로 부터 learn 2) MDP의 transition과 reward를 모름
- 다른점은 1) TD는 bootstrapping으로 incomplete epsiode로부터 learn함 → 즉 continuous하게 동작하는 환경에서도 사용이 가능함
- 2) TD는 guess로 guess함 → valu값을 업데이트하는데 다른 value값으로 업데이트 가능 → V(S(t)) = rt + rV(S(t+1)) , V(S(t+1))도 guess V(S(t))도 guess
- 다이나믹 프로그래밍에서도 이런식으로 이용됐으나 한 iteration에서 모든 정보를 가지고 제대로 된 업데이트를 한건데 TD는 지금 경험한 sample 내에서 partially 사용
- TD의 장점은 매 스텝마다 TD 업데이트가 가능하다는 것
2-1. MC와 TD

- MC의 G(t)가 TD에서는 R(t+1) + ΓV(S(t+1))로 대체됨 → 이유는 부트스트랩 하기 위해서
- Γ과 state 정보는 step마다 얻어낼 수 있고 그래서 업데이트가 가능함
- R(t+1) + ΓV(S(t+1)) 은 TD target이라 불림
- R(t+1) : 현재 State의 즉각 리워드
- ΓV(S(t+1)) : 부트스트랩 하기위한 값
-
TD error : TD타겟- V(S)(현재 state value function 값) → 베르만 equation에서는 이 둘이 같아야 하는데 수렴이 되지 않은 학습과정에서 다른 걸 TD error라고 함
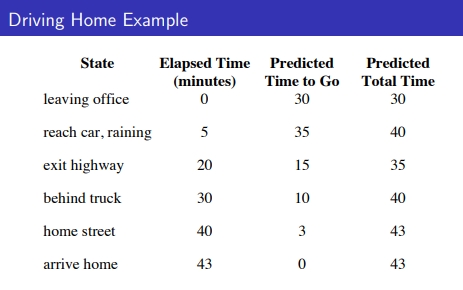
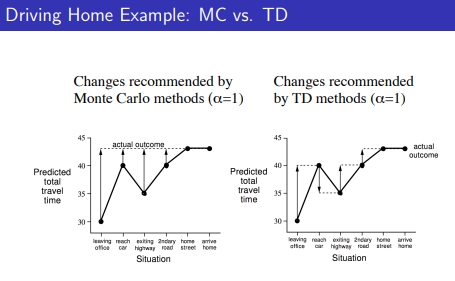
1) MC의 경우, home에 도착(terminal)까지 갔을때인 43을 기준으로 update를 진행
마지막 에피소드 값이 끝났을 때의 위치값을 각 state에서 도달하는 return 값으로 업데이트함
2) TD의 경우, state마다 업데이트 → MC의 차가 더 큼(variation이 큼)

1) MC는 complete sequence에서만 learn 가능 → episodic environments
2) TD는 incomplete sequence에서도 learn 가능
- final outcome을 알기 전에 learn 가능
- every step 후에 실시간으로 real time 학습 가능
-
continuing environments에서 작동 가능 → next v값은 r(S(t+1)로 학습 감마는 exponentially하게 적용된 감마 → 계속 더해지면 무한대로 갈 수 있는데 감마에 의해 그런 문제는 해결됨


1. MC : high variance, zero bias
1) 끝까지 간 값으로 update해서 variance가 있지만 unbiased함
2) good convergence properties
3) 초기값에 sensitive하지 않음
4) 이해 및 사용하기에 very simple
2. TD: low variance, some bias
1) MC보다 efficient (수렴시간)
2) function approximation에서 항상 잘 작동되진 않음 → 수렴이 잘 되지 않음
3) 초기값에 more sensitive
4) 학습의 과정에서 순간적으로 잘못된 값으로 update할 수 있음, variance는 낮음

2-2. Batch MC와 TD

- Batch(offlien): 환경에서 충분히 에피소드를 모았는데 그걸 일종의 dataset으로 보고 사용
-
K개의 에피소드를 모으고, K개 중 샘플을 반복적으로 뽑아서 MC 또는 TD를 적용

-
A와 B 2개의 State가 있고 랜덤하게 뽑아서 학습함 → MC와 TD 방식 적용했을 때 V(A)와 V(B) 값은 같을까? → 결과는 다름

-
TD는 베르만 equation을 사용하고 Markov strucure에서 사용, MC는 Markov property에서 작동되지 않음
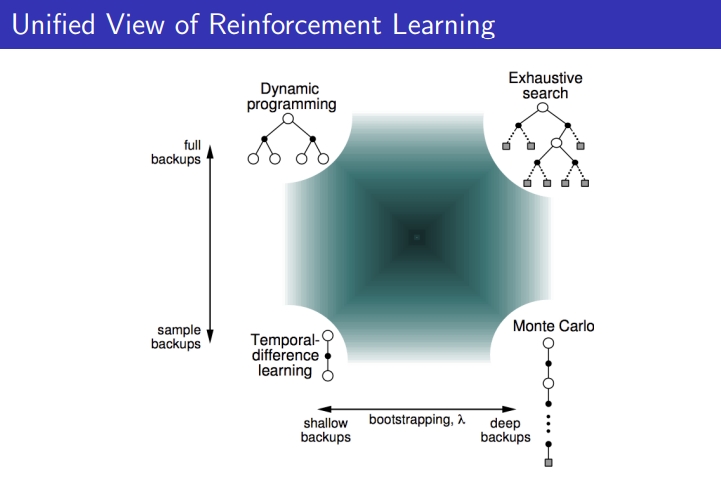
## 2-3. Unified view
### 2-3-1. DP VS MC VS TD
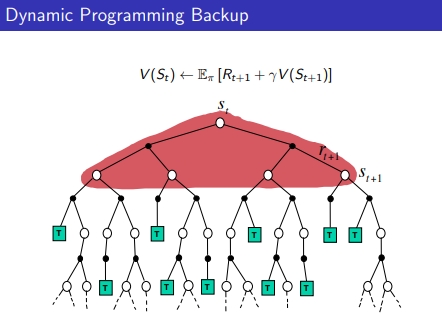
- 다이나믹 프로그래밍: 각 State의 기댓값 계산 가능 → B.E 성질 이용하여 → Full backup하여 모든 경우의 수를 계산하여 하나의 값 update
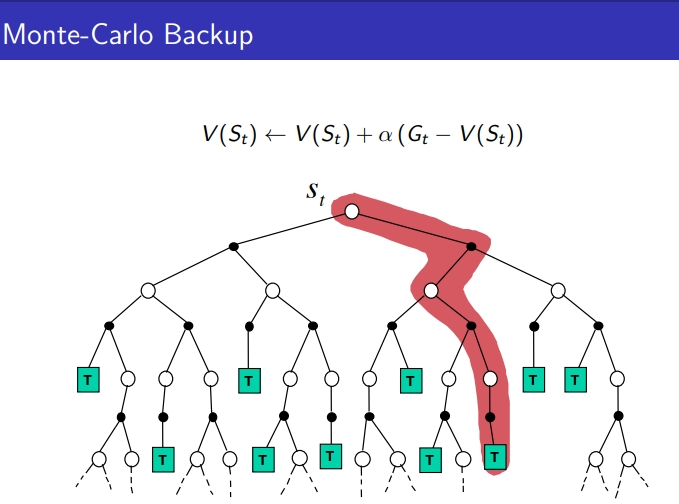
- MC: 시작점부터 끝까지 가고, 경험한 State의 각 G값을 계산해내며 update
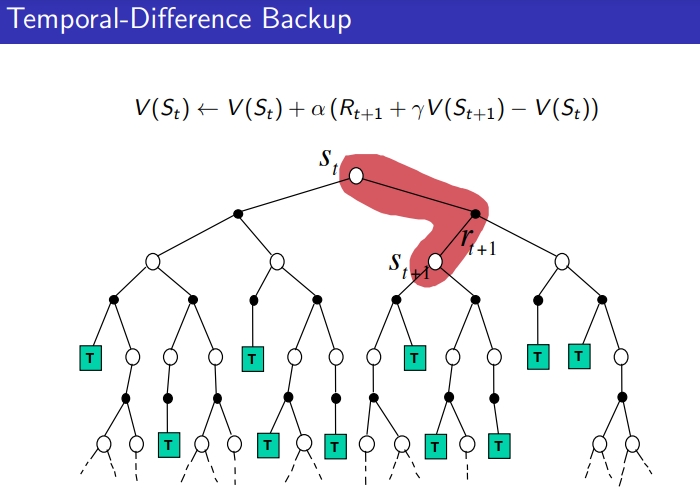
- TD: one step마다 경험한 걸로 bootstrap
### 2-3-2. Bootstrapping and Sampling
-
1. Sampling : information gather
- DP → sample X , model-based
- MC & TD → sample O, model-free
2. Bootstrapping: other estimates로 estimates를 update
- DP & TD → bootstrapping O, DP(known MDP), TD(unknown MDP)
-
MC→ bootstrapping X
2-4. n-Step Prediction
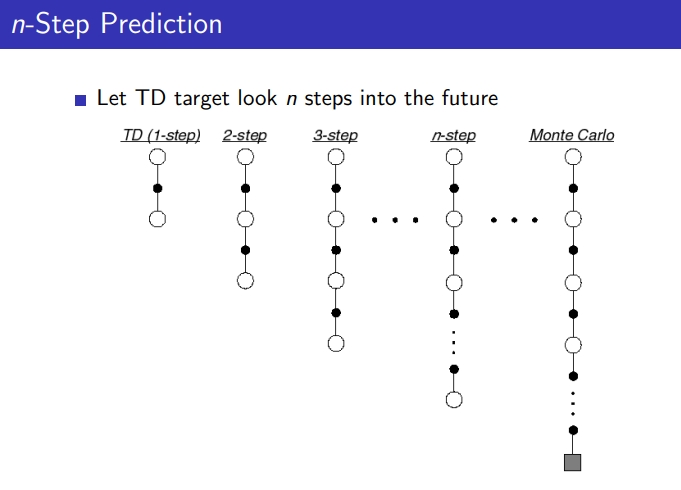
-
n step에서 TD값 update, 에피소드 끝까지 가서 update한다면 그건 MC와 동일

-
n step의 경우,n=4를 많이 사용하고 hyperparameter의 일종

-
그렇다면 n=2와 n=4 return을 평균해서 현재 V 업데이트 가능할까? 그게 λ-return
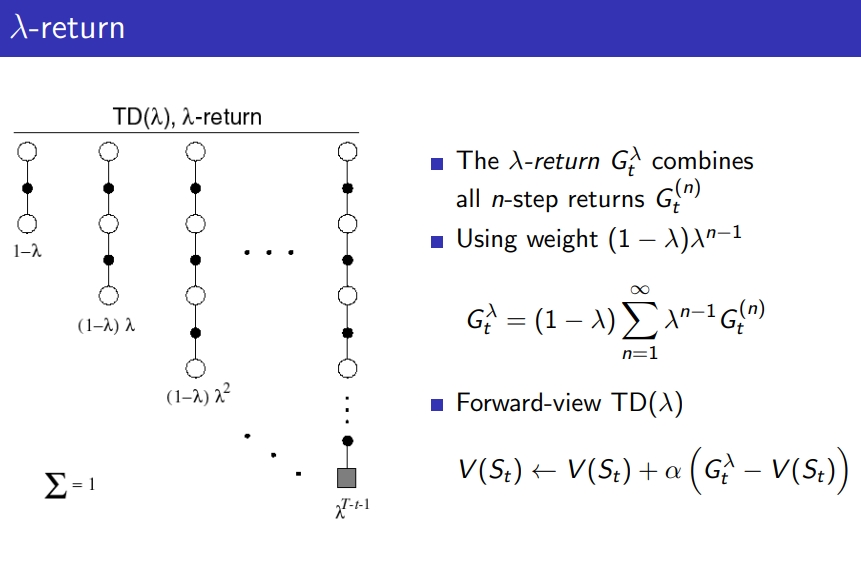
-
λ-return은 averaging n-step updates하는 것 ⇒ 각 step의 weighted average
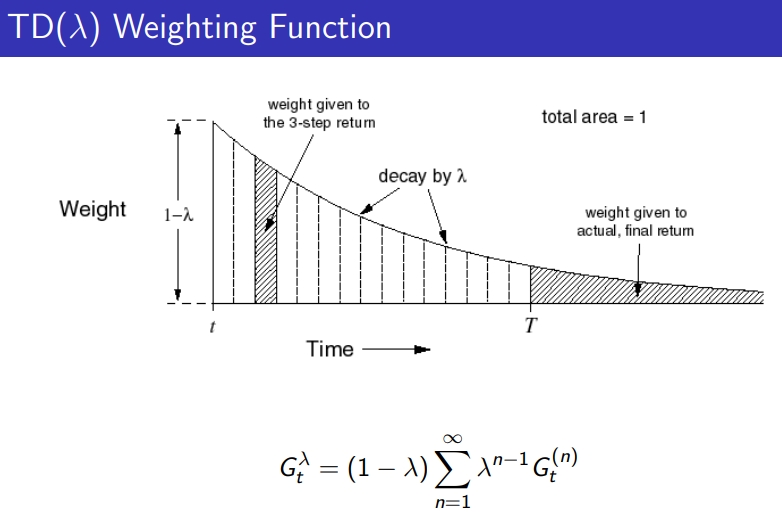
- λ=0이면, one step TD를 get, TD(0)
-
λ=1이면, MC를 얻음
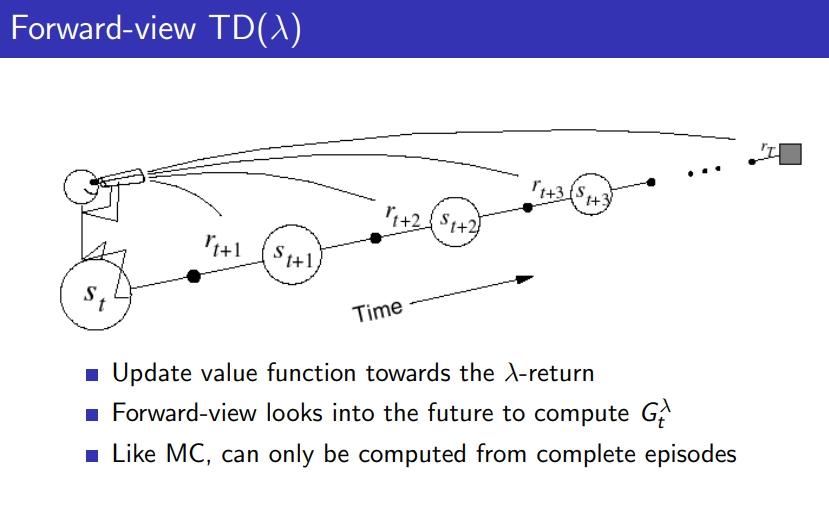
- 끝까지 가서 모두 weight줘서 반영 가능
- MC와 같이 끝까지 가서 계산 다하게 되는 특징
References davidsilver

Leave a comment