[강화학습] Model-free control

5. Model-free control

• model free control ⇒ MDP를 모르는 상황에서 value funiction을 점점 개선하는 방법, policy를 better하게 learn하는 것

  # 1. On-policy & Off-policy learning

  

1.On-policy learning

• 경험한 것을 기반으로 현재 policy 수정
• 주어진 policy로 experience를 수집하고 evaluation → improve policy ⇒ evaluate policy 반복
• 새 policy로 샘플을 수집하고 그 값으로 evaluation하고 upgrade하면 기존 sample을 버림→ sample efficiency 측면에선 좋지 않음

2.On-policy learning (=Q learning)

• 다른 policy에 의해 수집된 experience를 가지고 또 다른 policy를 평가

  

2. Generalized policy Iteration

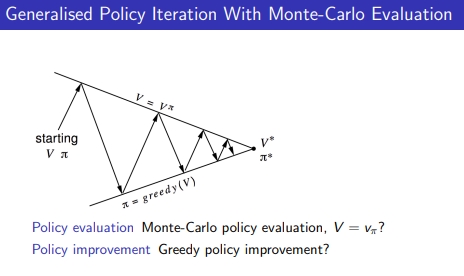
• 임의의 V, policy에 대해 충분히 evaluation하여 V 수렴 → greedy하게 policy extract & imporve

• evaluation과 improvement할 때 사용하는 알고리즘은 하나로 국한 되는게 아님

  

• MDP에서 improvement policy → V(S) → greedy하게 가는건 argmax를 취하는 것 → 어떤 액션을 했을 때 현재 state에서 즉각 리워드 + next stae의 value 값 * 감마 * transision matrix
• Model free에서 improvement policy →Q(s,a) →action stae value function → evaluate만 하려면 V(S)를 사용하면 되는데 improvement을 하려면 Q를 사용해야 함

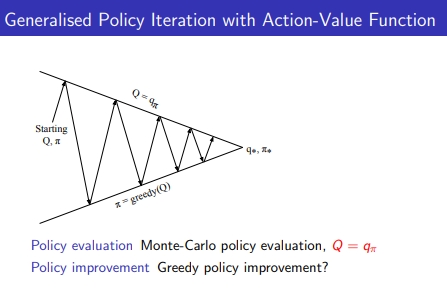
• 즉, MDP를 알 때 다이나믹 프로그래밍으로 policy greedy하게 improve → model free라면 improve를 이제 V→Q로 바뀜

3. Exploration

3-1. Exploration & Exploitation

• 강화학습은 trial & error learning
• 과거 경험으로 improve하는데 첫 경험으로 계속 같은 행동을 하면 안됨
• Exploration : environment에 대해 더 많은 정보를 찾는 것 → 과감하게 도전
• Exploitation: reward를 maximize하는 알고 있는 information을 ㅈ적용
• 이 둘의 balancing이 필요함

3-2. ε-Greedy Exploration

• 앱실론 Greedy
• m개의 action 갯수 존재 → 각 액션이 non zero prob을 가지도록 하자 → a1(0.7), a2(0.3), a3(0) 충분히 경험할 수 없음
• ε만큼 랜덤하게 행동해 → uniform하게 random하게 뽑음
• 임의의 ε에서 1-ε만큼은 greedy하게 action 취함 → state의 action별 q값의 argmax를 취함

3-3. ε-Greedy Policy Improvement

• 단순하게 greedy policy가 이전 policy보다 좋은 건 증명됨(π → greedy → π’) (Vπ’(s) ≥ Vπ(s))
• 모든 state에 대해 이전 policy의 value function과 새 policy의 value function을 비교하고 최소 같거나 value 값이 높아야 improve된 policy로 봄

• qπ(S,π’(s)) ≥ Vπ(s)

  ## 3-4. Variant Monte Carlo policy Iteration

  

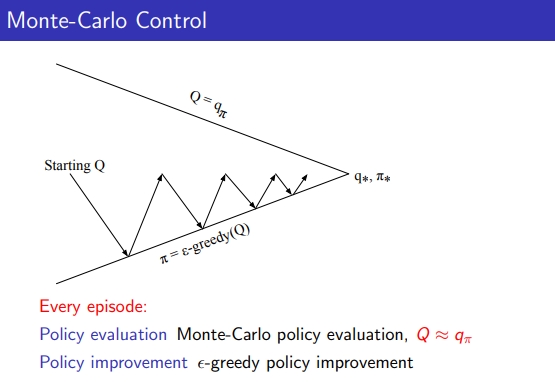
• 에피소드에서 얻은 experience로부터 ε-greedy로 upgrade할 수 있음
• 즉, 꼭 주어진 policy에 대해 어마무시하게 에피소드를 수행하여 evaluation이 완벽하게 수렴할 때까지 안해도 됨
• 많은 에피소드로 끝까지 evaluation하는 거 but 단 한번 에피소드 수행하고 그 에피소드 수행한 결과에서 ε-greedy도 policy가 improve되고 새로 얻어진 policy에 대해 한번에 evaluation 수행하더라도 MC policy iteration 가능

3-5. GLIE

• model free에서 무조건 optimal policy가 얻어질까?→ GLIE를 만족할 때만 가능함

1) 모든 state action에 대해 infinitley 반복한다면 무한에 가깝게 수행

2) policy는 점진적으로는 greedy policy로 감

ε를 adaptive하게 수정할 필요가 있음, 처음엔 큰 ε으로 시작했다가 줄여가면서 사용

k는 iteration 수이고 k가 크면 ε도 작아짐

• K번째 에피소드에서 다음과 같은 샘플을 얻고 에피소드에서 얻은 각 state, action마다 N값을 증가시킴, Q값은 incremental하게 반영

4. On-policy Temporal-Difference Learning

4-1. MC VS TD Control

• TD는 MC보다 advantage가 있는데 1) lower variance 2) online 3) incomplete sequences

4-2. SARSA

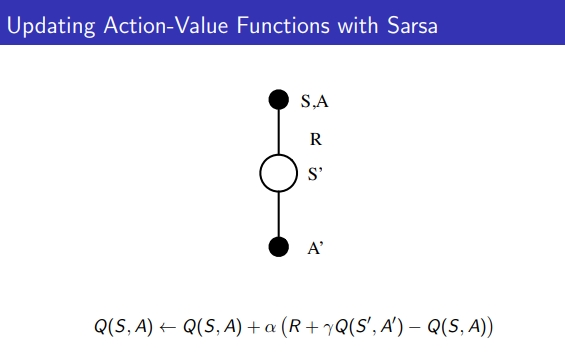
• TD기반 policy iteration을 SARSA라고 표현함

• 현재 state가 주어졌을 때 (S) → 어떤 액션을 하고 (A) → 리워드를 받으면 (R) → 다음 state (S)에서→ 한번 더 액션을 했을 때 (A)

  

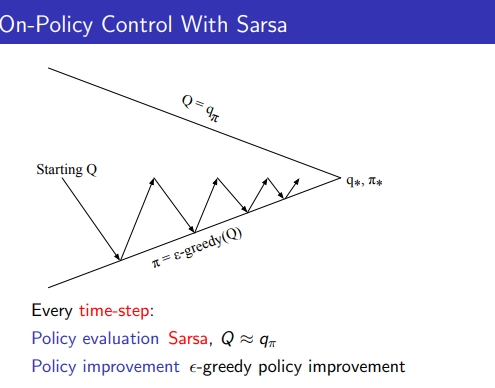
• 매 타임 step마다 알파 만큼 learning step으로 q값 업데이트

• 매 step마다 policy evaluation되고 ε-greedy로 policy improvement

  

1) 알파는 0과 1사이

2) Q(s,a) 초기화, terminal의 Q값 초기화

3) 첫 state를 초기화하고

4) state로부터 action을 가져오는데 ε-greedy 형태로 가져옴 → 이걸로 action을 취하고 R과 S’을 observe함

5) S’로부터 A’를 고름

6) SALSA로 Q 값 evaluate

5) 매 스텝마다 q값 업데이트

• SALSA도 TD 기반이므로 n step 사용

  ## 5. off policy learning

  

• observation sample이 다른 주체로부터 얻은 걸로 target policy를 update하고 싶음

• 전문가나 다른 agent, old policies, exploratory policy 로 부터 얻은 것

  ## 5-1. Importance Sampling

  

• off policy하는 방법 → 다른 dist의 expectation을 estimate
• P(x) :이 기댓값을 P에 적용하면 무슨 값이 될까
• f(x) : 수행하고 나온 값, sample의 기댓값 또는 다른 policy에서 얻은 값
• P(x)/Q(x) : importance weight
• Q(x) : 일반적인 동전 0.5, 0.5
• P(x): 구부러진 동전: 0.75, 0.25

• 확률이 다르면 다른 확률 동전을 무수히 던져서 E(x)~P[f(x)]를 얻을 수 있음, 그럼 얘를 재활용하고자 함

  ### 5-2. Importance Sampling - Off policy Monte-Carlo

  

• u라는 policy로 generate한 return 값이 있는데 이걸 policy를 evaluate하기 위해 사용
• 이 policy를 사용하면 각 weight return G값이 어떻게 달라지는 알고자 함
• U의 G 값이 있으면 policy로 해보지 않더라도 policy의 G값을 알 수 있음 → importance sampling 기법으로 → 즉, 새 policy로 V나 G값을 업데이트 할 수 있음
• U의 모든 값이 분모에 들어가기 때문에 0이 되면 안됨

• importance sampling은 많이 곱해지면 variance가 엄청 커질 수 있음

  ### 5-3. Importance Sampling - Off-policy TD

  

• V를 Q로 바꾸면 SALSA 가능

6. Q-learning

6-1. Q-learning

• importance sampling이 필요하지 않음
• next action을 가지고 오기 위해 u라는 behavior policy를 쓰는데 q learning에선 또 다른 target policy로 next action을 가지고 옴
• 다른 policy가 공존하는 형태로 q값 업데이트

6-2. off policy TD control

• behavior & target policies
• (현재) behavior policies u: ε-greedy
• (업데이트한 순간) target policies π: greedy

• Q learning target : 현재 즉각 리워드 + next state의 q max 값 가지고 옴

  

1) 어떤 S에서 ε-greedy로 A를 choose

2) A를 수행하고 R과 S’를 얻음 → Q값 업데이트

3) nest state의 가장 Q값이 큰 것을 선택

4) State만 업데이트 하고 위로 다시 올라가서 1)번부터 ε-greedy으로 action 수행하며 반복

6-3. Maximization Bias → Double Q learning

• Q learning이 max 값 취하는 특성으로 bias가 생기기도 함
• 일정 수 만큼한 Q는 일시적으로 bias가 있음, 무한히 하면 bias는 없을 것

Double Q learning → max bias를 막아주는 방법

• Q값을 두 곳에서 함께 사용 1) action을 select하는 상황에서 Q를 사용 2) 그 action을 해서 q를 estimate할 때도 해당 Q 사용
• 두 개의 Q→ Q1, Q2
• Q1 : max action을 선택할 때 사용
• Q2: value estimate할 때 사용

1) Q1과 Q2를 모두 initialize

2) S에서 ε-greedy로 A를 고름 → A를 실행하고 R과 S’를 관찰

3) 50%의 확률로 번갈아가면서 next state의 Q1에서 argmax에 해당하는 action을 가져옴, evaluation은 Q2r가 하면서 Q1을 업데이트 함 → Q1이 bias가 있더라도 Q2가 없다면 Q2에 의해 값이 낮아짐

7. Summary

SALSA & Q-Learning

[차이점1]

q-learning은 importance sampling 왜 사용 하지 않아도 되나? →

1) SALSA는 TD 타겟하려면 ε-greedy를 최초 action과 TD타겟 구할 때도 씀 → 다른 π에 적용하려면 importance sampling 필요

2) 반면 , Q-learning은 애초에 TD를 구할 때 ε-greedy를 사용하지 안쓰고 max를 가지고 옴 → 여기 액션이 다음번 iteration에서 쓰이지 않고 ε-greedy로 한걸로 씀(실제 환경에 영향이 없음) → 그래서 굳이 importance sampling을 안씀

⇒ TD를 구할 때 max로 구하는지 ε-greedy로 구하는지 → 그리고 이것이 다음 iteration에 쓰이는지 여부가 다름

[차이점2]

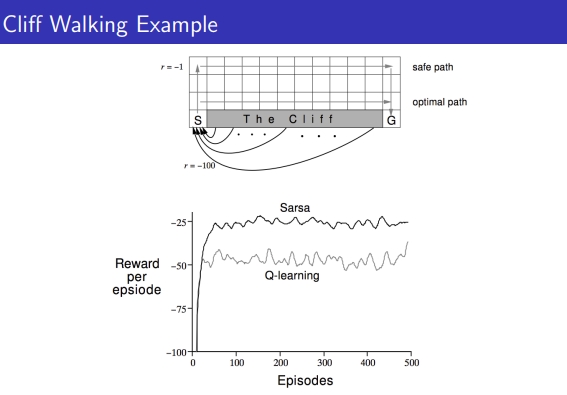
• 한칸씩 가는건 Reward -1 , 절벽에 떨어지면 Reward -100

Q는 optimal에 빠르게 도달하고자 하는 알고리즘으로 cliff walking에서 딱 붙어서 가서 한번씩 절벽에 떨어지고 SARSA는 안정적으로 위로 세이프하게 감. 그래서 로봇, 드론 등 안전하게 할 때는 SARSA, 시뮬레이터로 비용이 들지 않으면 Qlearning

Realtion Between DP & TD

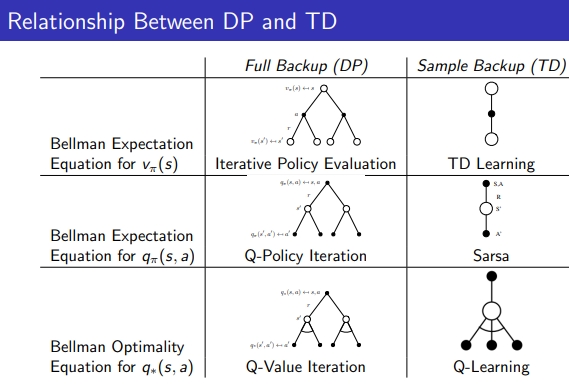
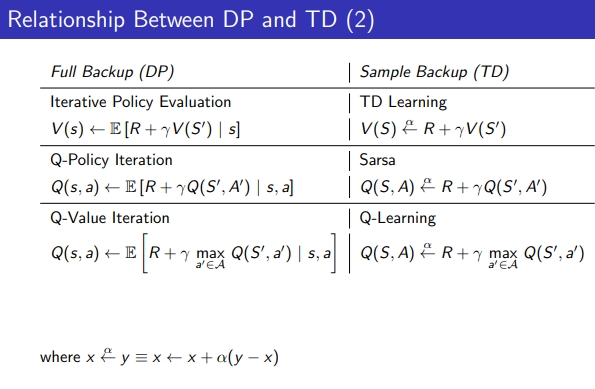
Referneces davidsilver