[강화학습] Policy Gradients

7. Policy Gradients (9장)

Review(value-based)

• Q learning에서의 large scale 문제를 해결하기 위해 Policy Gradients이 필요함
• DQN : Experience Replay, Fixed Target
• Double DQN : Reducing Overestimations
• Prioritized Experience Replay: selecting experience with a priority (TD 에러에 따른 priority)
• Dueling DQN : New Neural Network Architecture for DQN
• Multi-Steps, Distributional RL(q값을 분포로 뱉어 냄), Noisy-nets(state dependent exploration), and RAINBOW

Reinforcement Learning Algorithms

1. Value-based

• learned value function
• implicit policy (앱실론-greedy)

2. Policy-based

• No value function → policy를 바로 근사
• leaned policy

3. Actor-Critic

• Learned Value Function
• Learned Policy

Policy-based Reinforcement Learning

• 이전 value approximation에서는 파라미터 세타를 이용해 action-value function을 근사하고 이것을 이용해 policy를 generate함

  

• 이제는 policy를 직접 파라미터화함

  

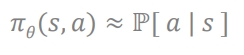
• model -free 강화학습(sampling)에 focus

Advantages of Policy-Based RL

1) Variance는 크지만 평균을 그어보면 수렴함 better convergence properties

2) high dimensional(액션 갯수가 많거나) continuous action spaces에 effective함

3) stochastic policies (DQN RN의 일부도 stochastic 하지만 DQN은 기본적으로 deterministic)

disadvantages

1) less stable during training process due to high variance(variance는 return값이 높았다 낮았다함)

2) sample inefficient(need more sample data) → value based는 off policy 가능, policy based는 on policy로 interaction

stochastic이 왜 필요한가?

• 가위바위보: DQN을 하면 주어진 s에서 Q(s,a1) , Q(s,a2), Q(s,a3) → max로 action을 뽑으면 → 쉽게 간파될 수 있음
• deterministic policy는 easily exploited하고 uniform random policy는 optimal함
• Value Based RL learns a near-deterministic policy → 앱실론을 가지고 탈출 가능성 있지만 그만큼 비효율적인 동작을 할 수 있음 → optimal stochastic policy는 앱실론 greedy보다 효과적으로 탈출할 수 있음
• Policy based RL can learn the optimal stochastic policy

Policy Search

• parameter 세타를 가지고, output이 a(optimal action에 대한 probability distribution) ⇒optimal policy를 찾으려고 함 : s가 주어지면 action에 대한 확률이 나오고 action을 뱉는 것

  

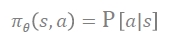
• policy π(θ)를 어떻게 improve하고 optimize할 수 있을까? → score function(J(θ))을 maximize하는 best parameter θ를 찾아야함

  

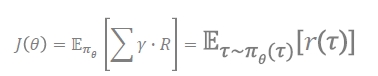
• expected return이 maximize 되는 것 → 모든 step의 reward를 더하는 걸 τ(타우)라고 함
• π(θ)를 improve하는 best parameter θ를 찾기 위해 policy gradient ascent 사용함

Policy Score(Objective) Functions

1) In episodic environments → start value를 사용할 수 있음

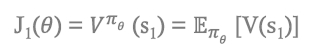
처음 시작하는 애는 value와 같고 기대치로 표현 가능

2) In continuing environments → average value를 사용할 수 있음

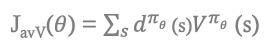
d^π(θ) : 각 state의 분포

V^π(θ) : 해당 state의 value

d^π(θ)(S) : stationary distribution of Markov chain for π(θ)

Policy Optimization

• J(θ)를 maximize하는 θ를 찾는 것 → gradient approach

policy gradient

• 기본적으로 ascent인데 -하면 descent
• score function을 maximize하는 건 = optimal policy를 찾는 것을 의미함

• J(θ) score function을 maximize하기 위해 gradient ascent를 함

  

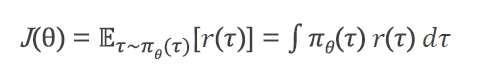
E는 sampling으로 가능 → gradient 하려면 θ에 대해 미분해야 하는데 r(τ)에 θ가 없어서 적용이 러여워서 바꿔줘야 함

• s의 act 확률이 expected return이 높은 값이면 gradient ascent로 해당 함수의 확률을 조금씩 높여주는 방향 → G가 낮으면 확률 낮아지는 형태 → 경험했을 때 G가 max되게 θ gradient ascent하게 함

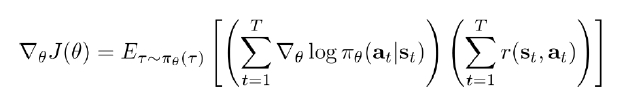
• 첫번째 괄호 : sample한 에피소드에서 시작부터 끝까지 갔을 때 사용한 해당 s의 action을 π(θ) 확률에 log 취해서 미분
• 두번째 괄호: 에피소드에서 T 갔을 때의 expected return

Policy gradient by sampling

1) sample 만들고 S → T까지 가

2) 그 sample로 return을 estimate하는 model을 fit함

3) policy를 improve하며 θ를 바꿈

Differentiable Policy Classes

• action이 뱉어지는 policy는 함수가 무엇인가요? value based는 argmax였고, policy는

1) Discrete → softmax

2) Continuous → Gaussian

• softmax는 θ에 의해 뉴럴네트워크를 만들어 output이 value 나오게 하고 value 값에 softmax취하면 다 더해서 1이 되는 policy 형태가 됨
• gaussian → s의 평균과 분산을 학습

Reducing Variance

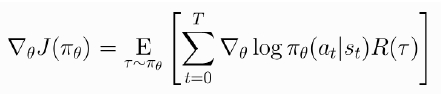
방법1: τ전체에 대한 return 값 = 모든 s에 대해 R(τ)가 곱해짐 → 이것이 variance 큰 것의 원인 : 전체에 대해 일괄적으로 곱하여 큰 영향을 줌

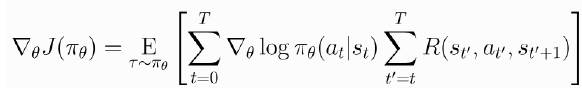
전체 T가 아닌 현재 보는 step t에 대해 t까지 오게 된 r이 아닌 t부터 끝까지 가게된 reward를 곱해줌 = reward to go

방법2: Baselines in policy Gradients

그때 그때 발생하는 R이 들쑥 날쑥 할 수 있어서 신뢰할 수 있는 baseline으로 빼주고 그 차이만큼만 영향을 주게 하자는 것 → 이 baseline이 bias를 주지 않음을 증명한 식 존재(최종적으로 baseline쪽 식은 미분하면 0이 되고 빼줘도 0이기 때문에 bias를 주지 않음)

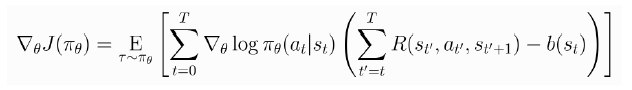
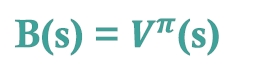
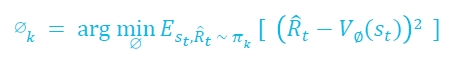
베이스라인을 이걸로 주로 사용함 → policy에 의해 얻는 단발성 R(t~T)와 baseline V의 차가 minimize시키는 parameter를 gradient descent하게 학습시킴

Vanilla Policy Gradient Algorithm

Actor-Critic

• value function과 policy를 둘 다 학습함 → hybrid 형태
• value function은 비평가 역할을 함 discount return을 maximize
• 단순 policy로 하면 variance 커서 Vanilla Policy Gradient까지 가면 V(s) 등장 → 그러나 특성이 한 에피소드 끝날때까지 쭉 환경과 소통하고 그리고 그때 얻어진 reward to go 값을 역순으로 계산해서 value function인 baseline을 기반으로 variance를 줄이는 형태
• policy gradient는 한 에피소드는 끝나고 reward가 유사할 수 있지만 마이크로레벨로 잘했다 못했다는 알 수 없음 → 관건은 episode하게 해야하나?임

About Choosing the target

• baseline을 쓰긴 하지만 크고 복잡하면 high variance 문제가 사라지지 않음
• Vanilla에서는 value function을 reward to go와의 값을 빼서 min으로 씀→ 이는 부트스트랩 개념은 아님(V(St) ← R + V(S(t+1))
• 이제는 value estimate와 부트스트랩을 사용하겠다
• step마다 critic을 함 → action value function을 estimate함
• critic은 action value function parameter w를 업데이트하고, Actor는 policy parameter π(θ)를 업데이트 함
• π에 의해 행동할 때의 Q를 근사하려는 파라미터 w

• θ는 critic이 suggest하는 방향으로 학습

  

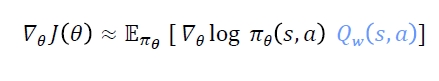
• 예전에는 R 또는 R-V였는데 이제는 Q를 근사함(R과 R-V는 에피소드 끝났을때 학습, Q는 매 스텝마다 업데이트 가능)
• Q 값이 높으면 해당 액션을 더하려고 할 것이고, Q 값이 낮으면 그 액션을 덜하려고 함
• advantage function은 policy gradient의 variance를 줄일 수 있음

• Variance를 줄이려고 벨루, q, q-v 등 다양하게 제안

  

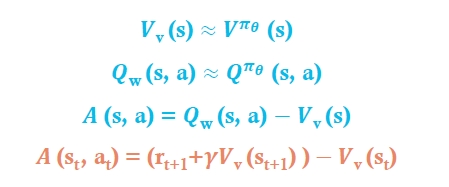
• 1) 환경에서 관측으로 state 정보를 얻고
• 2) 그 S로 부터 π(θ)로 a(t) 선택
• 3) actor: 매 타임스텝마다 어떤 a를 선택했다는 정보를 가리고 termination을 계산
• 4) a(t)로 환경에 영향을 주고 next state와 next reward를 가져옴
• 5) critic: 매 타임 스텝마다 현재 s, next s, reward를 가지고 critic을 만듦
• every step마다 policy도 비평 가능, θ도 업데이트 가능
• Actor Critic Algorithm은 매 스텝마다 부트스트랩을 활용해서 θ에 대한 네트워크 w에 대한 네트워크를 사용함

A3C: Asynchronous Advantage Actor-Critic

• GPU를 사용하지 않고 parallel actor-learner를 함
• N step은 policy와 value function을 업데이트함
• continuous와 discrete action space에서 모두 작동됨
• env가 랜덤하면 시작 S(0)이 다를 수 있겠지 → n개의 learner(worker) 각 worker가 environ과 parallel하게 상호작용하여 학습하고 → 각 worker가 올려주는 gradient를 평균적으로 학습시킴 그리고 글로벌 네트워크가 다시 gradient 업데이트 해서 내려줌
• 각 worker의 경험하는 에피소드의 길이가 다를 수 있고 이로 인해 다양성이 있을 수 있음 sample 간 correlation 문제를 해결할 수 있고 또 다른 parameter로 앙상블 효과를 낼 수 있음
• worker가 envion과 interact를 하고 worker가 value와 policy loss를 계산하고 worker가 loss로부터 gradient를 얻음 → worker는 gradient로 global network를 업데이트함

A2C: synchronous Advantage Actor-Critic

• A3C는 여러 에피소드를 경험하다보니 각 worker 중에 과하게 느리거나 빠른 애가 들어가서 문제가 생기고 성능에 영향을 줄 수 있음
• A2C는 coordinator가 한 에피소드를 할당하고 각 worker가 그걸 알아서 update
• converge가 빠르다고 함

Summary : Policy-Gradient

•REINFOCE : Policy-gradient + Reward To Go •Vanilla Policy-gradient : REINFOCE + Baseline •Actor-Critic : Vanilla Policy-gradient + Critic (Bootstrapping) •A3C : Actor-Critic + Asynchronous + Advantage + N-step •Synchronous Version of A3C

Policy Gradient and Step sizes, Trust Region

Trust region policy optimization

• step size는 일종의 learning rate
• policy를 얼마나 update하면 안정적으로 증가할까?
• supervised learning에서는 step size가 큰 영향을 주지 않음(너무 크더라도 다른 미니배치 데이터로 업데이트하면서 과하게 업데이트 된건 돌아오곤 함→ 한번 과한 경우가 있더라도 돌아오는 경향)
• RL에서는 step이 너무 크면 policy가 나빠지는 현상이 있어 policy로 시행착오 → 과하게 얼토당토하지 않은 data를 얻어서 헤어나오지 못할 수 있음
• update policy가 좋다는걸 보장하길 원함 → 큰 스텝, 작은 스텝 등 어느정도의 영역 안이면 떨어지지 않을까하는게 trust region

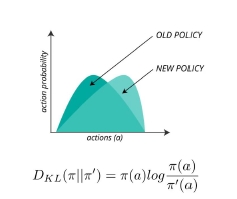
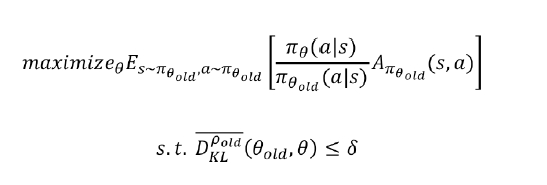
• 이전 policy로 얻은 s,a의 확률값 p /지금 구한 new policy의 확률값 p
• 과한 step이 아니도록 old와 new의 확률 분포가 너무 벌어지지 않도록 함

PPO (Proximal Policy Optimization)

• TRPO 기반 휴리스틱 알고리즘 → 아카데믹적인 기여는 낮은편이지만 practical함
• PPO는 discrete & continuous 모두 가능 (continuous는 최근에는 SAC이 더 잘 나온다고함)
• 한번 얻은걸 online 형태로 반복학습함

• TRPO는 step size 이슈를 지적해서 trust region을 찾아 증명을 잘 한건데 → computation 구현하려고 할 땐 휴리스틱한 형태로 PPO로 사용

  

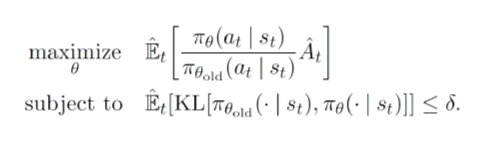
Clipped surrogate objective

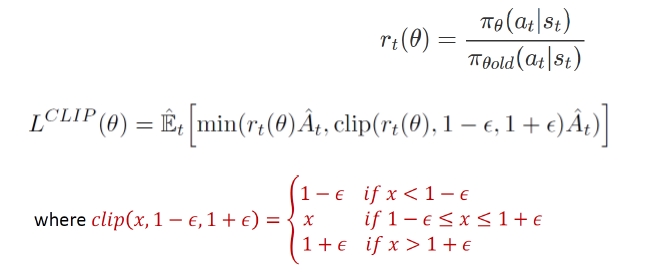
• 두 policy의 차이를 10,20% 등으로 clip시킴 → TRPO에서 복잡한 s.t.로 주려고 한걸 간단하게 clipping으로 줌

ver1.

• 1) T번 만큼 쭉 에피소드를 진행하고 s,a,r,p(a

  s) 정보를 저장하고

• 2) 그리고 나서 trajectory 각 정보에 대해 surrogate function을 구하고 SGD하여 θ 학습
• 3) epoch 여러번 해도 clipping 하기 때문에 큰 문제 발생하지 않음 → sample efficiency 올림
• 4) convergence 될 때까지의 반복

ver2.

• 1) 한 agent로 t개만큼의 time step을 모아서 몇번 epoch를 학습하는 형태 또는 parallel 하게 적용 agent1

  agent2

  …. agent 각 timestep을 뱉어내게 되면 일종의 배치 형태로 여러번 epoch을 학습할 수 있는 버전

• 2) convergence 될 때까지의 반복

-PPO가 대부분 빠르고 학습 결과 좋았음, DQN보단 좋은데 rainbow다 좋다는 아님 상황에 맞게 선택