[강화학습] value function approximation

6. value function approximation, Advanced Value Function Approximation (7장~8장)

지금까지의 요약

1) true model을 모르는 경우 → policy improvement를 generalized함, explration의 중요성

2) Model free control with Monte Carlo(MC)

3) Model free control with Temporal Difference(TD) → MC는 variance가 높아서 TD를 많이 사용

• SARSA (on policy) : 앱실론-policy 사용(action과 TD 구할 때 모두)
• Q - learning (off policy): 앱실론-policy → action , greedy → TD 구할 때 ⇒ Q learning은 maximize bias가 있어서 double Q learning 사용

Q table의 한계

• real 환경에서는 Q table이 복잡해짐

→ model free RL에서 Scale을 어떻게 높일 수 있을까?

→ value function approximation : value function을 Q 테이블로 접근하지 말고 V나 Q를 approximation하자 → V나 Q를 함수로 보고 근사할 수 있다고 보자

1. Value function approximation

1) 지금까지는 value function을 lookup table로 represent함

2) large MDP의 문제: 메모리에 저장되어야 할 많은 state나 action이 있다, 각각의 state의 value를 learn하는 건 매우 느림

3) solution: deep neural network(paramterized function)으로 function approximation을 통해 value function을 estimate함

Benefits of Approximation : compact representation

1) memory를 reduce

2) computation을 reduce

3) explore할 experience를 reduce

Feature-Based Representations

• features의 vector을 사용하여 state를 describe

features는 state에서 real number까지의 fucntion

예전에는 사람이 feature를 계산했지만 이제는 이런 input 특징 찾는 것도 뉴럴 네트워크에 맡기고자함

2. Linear Value Function Approximation

1) value function을 feature에 대한 linear combination으로 represent

• S: state
• w : parameter vector
• Xj(S)*Wj : Xj(S) 어떤 state가 주어졌을 때 픽처 벡터를 뽑아내고 weight(Wj)를 곱함

2) true value V(s)와 approximate인 V(s,w) 사이의 mean squared error를 minimize하는 parameter vector w를 찾아냄

• loss함수를 mininmize하게 해서 w를 점진적으로 찾아냄

3) Gradient descent는 local minimum을 찾아냄

3. Incremental Methods

Incremental Prediction Algorithms

• 처음엔 optimal value function을 모르지만 supervisor에 의해 true value fucntion을 assume
• 그러나 RL은 supervisor 없고 only reward만 있음 → value를 다음으로 target들로 대체
• MC는 target을 return G로, TD는 target을 TD target으로 넣음

Incremental Control Algorithms

• feature vector에 의해 state와 action이 represent (임의의 s가 들어갔을때 s에 대한 feature vector가 있다고 가정했을때 q함수는 linear 형태로 정의 가능)
• features의 linear combination에 의해 action-value function이 represent
• Xj(S,A) : state에서 action 했을 떄의 feature vector

• value function을 approximation 하듯이 action value fuction approximation

  

• target을 대체함
• SARSA : next action 앱실론

• Q-learning : next action G

  

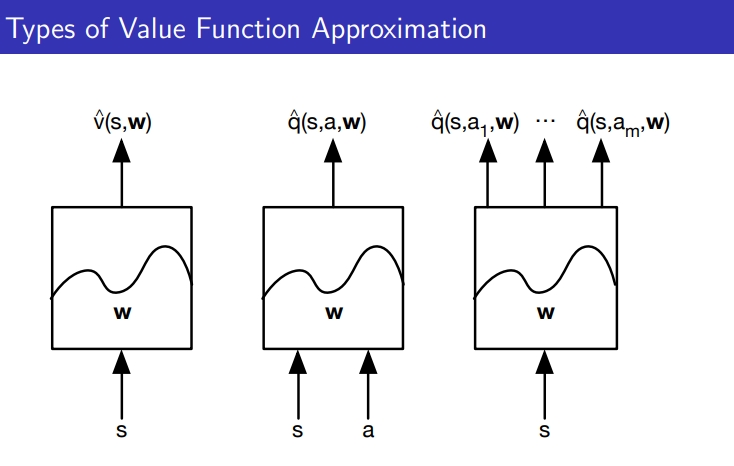
1) V(s,w) : s를 입력하면 black box에 들어가서 s에 해당하는 value 값 뱉어짐

2) q(s,a,w) : s와 a를 입력하면 q값 산출

3) q(s,a(1), w) ,…., q(s,a(m), w) : s를 입력하면 s의 action 별 q값을 뱉어냄

4. Deep Reinforcement Learning

Review: Neural Network

• weighted edges와 연결된 computational neurons(units)의 network
• 각 unit(computational neurons) computes: z = h(xw+b)
• h: activation function→ hidden layer 깊어지고 width 넓어질 수록 값이 폭발하는 걸 해결하려고 non linear 사용 ex) relu
• (xw+b): weight vector
• neural이 좋은 이유가 S가 input되면 compact하게 representation을 잘함, 조금 다른 s’가 들어와도 주요 특징이 매우 비슷하게 뽑혀져서 비슷한 액션을 하는 여지를 줌, 또한 continuous의 경우 모두 하나 하나 학습하는게 아니라 어느정도 학습경험을 하면 그 사이 state는 행동 추론 가능

Deep Reinforcement Learning

1) represent하기 위해 deep neural network 사용 → value fucntion , policy, model

2) optimize loss function by SGD

Deep Q-Networks (DQNs)

• state-action value function을 weight w의 Q-network으로 Represent
• raw한 s를 입력→ wS(t) : s에 대해 action 갯수만큼 output이 나옴

Deep Q-Network Training

• S(t)를 넣어서 내가 선택한 액션에 대한 Q-prediction get→ wS(t)
• S(t+1) next s를 넣어서 한번 더 prediction 값 중 max 값 → wS(t+1)

Example: Cartpole

• state: 각도, 각 속도, 포지션, 좌우 움직이는 속도
• action: 계속 오른쪽 왼쪽으로 움직이기
• reward: 각 step마다 떨어지지 않고 살아있으면 1, 일정이상 바뀌면 done

5. Convergence Issues

• 딥마인드가 지적한 문제 → convergence가 잘 되지 않는 이슈가 있음 → q함수를 ground truth와 차이를 줄이려고하는 convergence가 잘 되지 않는 이유 2가지

1) Correlation between samples: 샘플들 간의 correlation이 높음

• 샘플에 잘 fit되는 approximation 함수를 찾아보자 하는데 한번에 모든 학습 set이 주어지면 용이한데 초반에 입력된 sample만 학습되면 전체 대비 bias됨
• cart pole을 보면 초반 경험 sample의 corr이 큼 ( 처음 s와 그 다음에 얻은 것들이 유사)

2) Non-Stationary targets = moving

• guess로 다른 guess를 update함
• prediction Q를 update하면, target Q가 영향을 같이 받음
• Q = Q(S(t), A(t), w) ⇒ 이 w가 gradient descent로 update 됨 → target(Q(S(t+1),a,w)도 동일한 w를 쓰기 때문에 q 값이 같이 증가하거나 감소하여 간격이 줄어들지 않음
• target Q와 prediction Q를 분리할 필요가 있음

6. Deep Q-Networks(DQN)

• 3가지 솔루션

1) Deep Neural Networks

2) Experence Replay

• solving correlations between samples

3) Fixed Target

• solving non-stationary targets

1) Deep Neural Networks

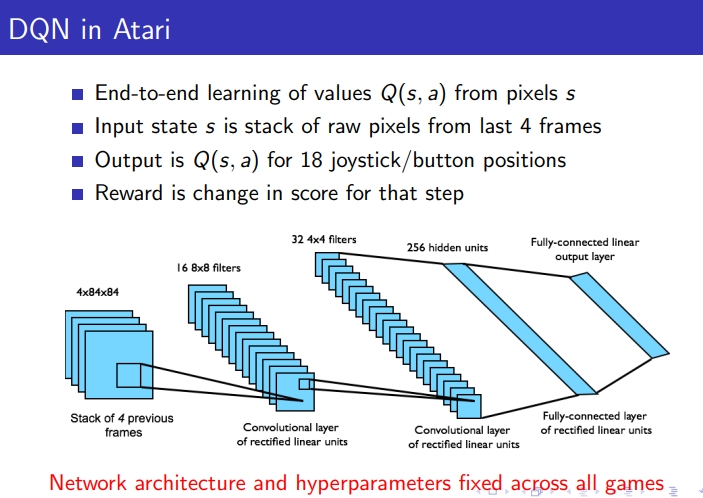
• 아타리는 49가지 게임이 있는데 DQN의 장점은 단 하나의 알고리즘으로 49개의 게임 진행

2) Experience Replay

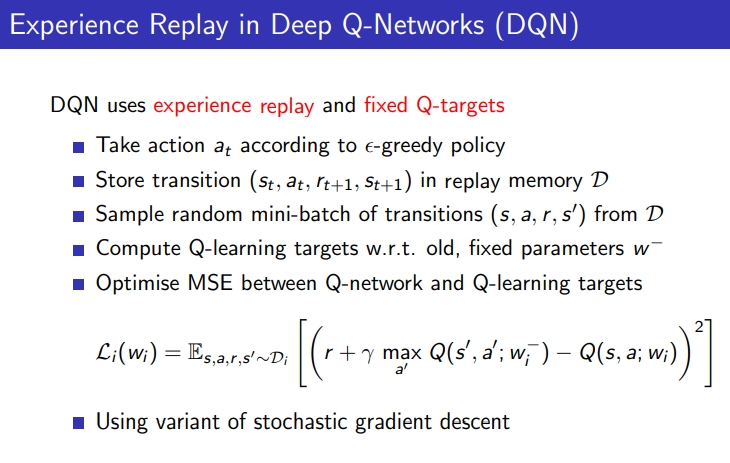
• correlation을 없애기 위해 agent 경험 샘플을 적극 재활용

1) 앱실론 greedy policy에 의해 action을 취함

2) experience (s,a,r,s’)을 replay memory D에 store

3) 어느정도 쌓이고 D에서 랜덤하게 mini batch 함 (D에서 랜덤하게 뽑아)

• 초반 경험에는 action 취하고 store만 하고 학습을 하지 않는 경우도 있음 일정 이상 replay memory가 찰 때까지
• w에 의해 q값이 업데이트가 되고 q 기반으로 앱실론 policy가 더 똑똑해지고 policy에 의해 모아지는 새로운 experience가 이전 랜덤 experience보다 좋을 수 있어서 초반에 쌓인걸 방출하고 넣어줌
• generalized된 뉴럴 네트워크 모델을 편향없이 학습시키는데 도움을 줌

3) Fixed Target

• q 네트워크를 2개 만들자 (Q-prediction, Q-target)
• Q prediction은 current S, A에 대해서 실제 predict한 값을 가져오는 용도
• TD 타겟은 똑같은 모양의 타겟 네트워크에서부터 가져옴
• 똑같은 뉴럴 네트워크인데 들어가는 weight가 다름(w, w-)
• 차이를 줄어들게 Gradient Descent하는데 w가 변하고 w-는 아무것도 하지 않아서 변하지 않음 그래서 둘 사이가 좁혀짐
• 평소에 w만 학습시키다가 일정 이상 학습 시키면 w를 w-로 그대로 복사

DQN : experience replay & fixed target 접목

DQN summary

1) DQN은 experience replay와 fixed target을 사용

2) replay memory D에 store transition(앱실론 policy로 수행한 experience를 모음)

3) sample random mini-batch of transitions from D

4) compute Q learning targets, fixed parameters w-

5) Q-network와 Q-learning targets 사이의 MSE를 optimize

6) Used SGD

---

---

Advanced Value Function Approximation

Review: Deep Q-Network

1) Q-learning은 table이 커진다는 이슈가 있음: 저장공간 & 모든 계산에 대한 이슈

2) DQN은 근사해보자는 개념이고, 계속 학습해서 feature를 뽑고 계산량을 줄이려함

3) 2가지 문제인 (1) sample 간 correlation (2) Q 값 업데이트를 해결하기 위해 DQN은 experience replay와 fixed Q-target을 사용

4) Replay memory에 transition (S(t), a(t), r(t+1), s(t+1))을 store함

5) D로 부터 transition에 대한 random mini batch를 함

6) Q learning target과 fixed parameter를 compute함

7) Q network와 Q learning target 간의 MSE를 optimize함

8) Stochastic gradient descent를 사용함

9) Q network: 액션을 뱉는데 필요한 prediction

10) Target Q network: TD 타겟

Advanced Value Function Approximation

1) Double DQN

2) Priortized Replay

3) Dueling DQN

1. Massively Parallel Methods for Deep Reinforcement Learning

• 단일 머신 아니고 parallel
• DQN은 single machine으로 적용했기에 atari game에 12~14일 정도의 long training time이 걸림
• Deep learning computation이 parallelized 할 수 있음
• RL의 unique한 property

Google Reinforcement Learning Architecture(distributed Architecture)

• Actor: 여러 개 프로세스가 동시에 생성되서 각각 환경과 interaction하는 actor라는 역할을 담당하는 프로세스가 있음
• Replay buffer: 동시다발적으로 얻어낸 경험을 Replay buffer로 저장
• Learner: 동시다발적으로 Q network와 Target Q network 진행
• Parameter Server : Q network에서 학습한 결과를 올리기
• Actor, Learner, Parameter Server 3가지가 분산임
• Single DQN은 12~14일 소요, Gorila DQN은 6일 걸렸고 outperfom함
• Gorila DQN은 deep reinforcement learning에서 최초로 대규모 분산학습 환경을 제안해본 연구임
• Gorila DQN은 분산된 replay memory와 분산된 neural network를 이용해서 act와 learn을 parallel하게 진행함
• Gorila DQN은 time은 줄이고 성능은 높임
• 하지만 Gorila DQN의 resource는 231이었고 DQN은 1로 가성비 측면에서 좋은 건 아니었음

2. Multi-Step Q-Learning

• n step은 Q learning의 n-step 구현과 거의 유사함

3. Double DQN

• 1) action을 뽑을 때 argmax→a , 2) Q 값 evaluate/업데이트 할 때도 max를 취함 ⇒ bias가 maximize됨
• 즉, Q learning의 단점은 overestimated values를 select하기 쉬우며, bias가 maximization 되기 쉬움
• 이를 해결하는 게 double q learning: Q table 2개로 Q1은 prediction Q2는 target
• 한 함수로 action을 취하면 그 action에 대한 q값을 가져오는 건 다른 q함수임
• DDQN은 overestimation을 reduce함
• DQN은 추가적인 target network를 가지고 있으니까 그래서 더 DDQN이 쉽게 차용됨
• next state의 argmax는 Q1으로, value는 Q2로 진행
• DDQN의 현재 Q network(w)는 action을 선택하고, older Q network(w-)는 action을 evaluate함
• 현재 Q network(w)는 action을 뽑고, action에 대한 q값은 w-로 가져올 수 있음
• w-를 가지는 타겟 Q에서 먼저 argmax로 action 하나를 뽑고, 타겟 q인 w에서 이런 state와 action을 가졌을 때의 q값은 얼마인지를 계산
• 실제로 DQN과 DDQN을 비교해보면 DQN은 값이 overestimate해서 값이 올라가고, DDQN은 수렴하는 듯한 그래프가 나옴
• DDQN은 더 stable하고 reliable한 learning을 함
• DDQN은 additional network 없이도 existing DQN architecture를 사용함
• DDQN은 single DQN보다 성능이 좋음

4. Prioritized Experience Replay

• 기존 Replay Buffer는 과거 경험을 모아두고 실행을 진행해서 랜덤 샘플링으로 correlation을 완화시키고 experience를 재사용함 → sampling 방식은 uniform하게 진행됨, siginificance에 관계 없이 동일 확률로 진행됨 ⇒ experience의 중요도를 반영할 가치가 있지 않을까?라는 질문에서 PER이 나오게 됨
• 중요도는 Temporal-difference(TD) error로 측정함 → TD error가 클수록 우선순위를 줌 → Greedy TD-error prioritization → experience replay에서 TD error 값으로 sorting하고 샘플링은 가장 위에서부터 가져옴 → 또 바뀐 걸 넣고 resorting하는 식으로 진행함

Stochastic Prioritization

• Greedy TD-error Prioritization의 단점은 low TD-error인 experience의 경우, 긴 시간 동안 replay가 되지 않을 수 있음, 또한 초반에 noise로 큰 TD-error를 가진 experience가 bias로 계속 나올 수 있음 ⇒ 이를 해결 하기 위해 stochastic monotonic sampling을 제안함 → non zero probability를 gurantee함

  

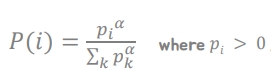
• experience sampling의 probability는 P(i) = priority/(모든 experience의 priority를 다 더한 값)
• 알파는 일종의 hyperparameter로 알파가 0이면 random uniform이고, 알파가 1이면 priority에 비례해서 확률이 정해짐
• priority를 정하는 2가지 방법이 있음

• 1) option1: proportional prioritization → TD error를 절대값으로 주고 0이 되지 않게 아주 작은 앱실론을 주기

  

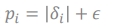
• 2) option2: rank-based prioritization ⇒ rank로 1등이면 1/1, 2등이면 1/2 rank가 높을 수록 높은 priority

  

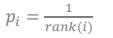
Annealing the Bias

• prioritized replay는 bias를 야기시킬 수 있는데 experience distribution을 바꾸기 때문이며, 이러한 bias를 보정할 필요가 있음

• 이러한 bias를 Importance-Sampling(IS) weight를 방법을 사용하여 보정할 수 있음 → IS는 non uniform probabilites를 compensate할 수 있음

  

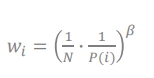
→ 1/N은 uniform이고 1/P(i)는 우선순위 ⇒ w는 교정을 위한 weight

• 중요도를 반영하되 w를 통해서 그 수준을 조정함→ B를 처음에 1로 줬다가 줄여가면서 w를 줄이는 효과를 줄 수 있음

  

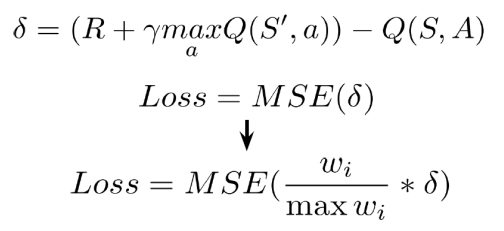
• 특정 experience가 빈번하게 sampling이 되었다고 하면 w를 좀 더 적은 portion으로 주어서 조정함
• priority를 기반으로 확률을 새롭게 만들어서 그 확률에 따라 experience를 sampling함
• PER은 learning을 좀 더 efficient하게 할 수 있음, learning 속도도 2배 이상 빠름, Single machine으로 해도 atari에서 성능을 향상시킴

5. Dueling Network Architetures for Deep Reinforcement Learning

• DQN은 feature extraction을 하고 dense layer를 통해서 각 action별 q값을 뱉어냄
• dueling은 2개의 separate network (1) V(s) (2) Advantage value 값 ⇒ Q값 = (1) +(2)
• Advantage value : s가 특정 a에 대한 advantage value 값
• common CNN module을 공유해서 state value와 action advantage를 분리해서 학습시키고 이후에 aggregating layer을 통해 Q function을 생성함
• V(s) 자체가 너무 커서 action Q(s,a1), Q(s,a2)의 차이가 크지 않으면 학습이 잘 되지 않을 수 있기 때문에 분리함 , 분포가 상이하면 학습이 잘 되지 않음 그래서 zero mean normalization을 많이 한다고 함

• 원래는 Q(s,a1), Q(s,a2) 등이었는데 1) S가 무슨 action을 하느냐에 상관없이 V(s)를 알고자 하고 2) 그 S가 각 action을 했을 때 그 action이 어떤 value를 가지는지 A(s,a1), A(s,a2)를 구하고 1)과 2)를 더해서 Q를 구함

  

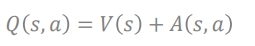
• Q(s,a) = V(s) + A(s,a)
• V와 A를 각각 정확히 판별해 내기 어려움 ex) Q가 5라고 할 때 1+4 인지, 2+3인지 모호한 상황임
• 이러한 문제를 해결하기 위해 2가지 옵션이 있음

• 1) 현재 s의 v+ 지금 선택한 advantage - 해당 s의 존재할 수 있는 advantage의 max값

  

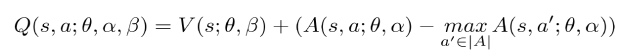
• 2) use mean as baseline : 현재 s의 v + (지금 선택한 advantage - 해당 s의 존재할 수 있는 모든 advantage의 평균)

  

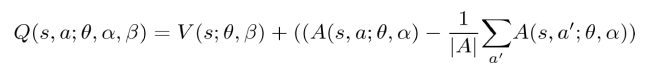
• V는 장기적인 시각, advantage는 근시안적인 것에 attention
• DQN의 경우, action만큼 q값을 가져야해서 추론할게 많고, 쓸모없는 action이 있을 경우 정도가 심해지고 학습시간이 많아짐 dueling은 advantage를 별도로 봐서 불필요한 action은 신경을 쓰지 않아도 됨 핵심 action에만 attention하는 경향이 있어 빠르게 학습이 가능하다고 함

6. Distributional RL

• General RL: Q(s,a) deterministic한 policy였다면 단일 스칼라 값이라 greedy한 선택이 가능함
• Distributional RL: Q함수가 분포를 가짐 그 상태에서 action Q 값을 계속 보니 stochastic하는 분포로써 표현의 다양성이 제공됨
• Bellman Equation → Distributional Bellman Equation

7. Noisy Network

• exploration에 집중
• model free는 sampling 기반이 여기서 더 중요함 복잡할 수록 더 중요

• 앱실론 greedy보다 효과적인 exploration이 있을까? → 앱실론-greedy는 랜덤하게 해서 이론적으로는 모두 갈 수 있지만 large scale behavior에서는 모두 가는데 시간이 많이 걸릴 수 있음 → Neural network + perturbation : 뉴럴 넷에서 noise 넣어서 자동으로 exploration , state dependent exploration이 있는데 → 주어진 s에 대해서 너무 뻔한 s에 대해선 exploration 하지 않음

  

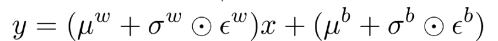
• 노이즈가 반영된 Q 값 = y = wx+ b ⇒ y = (평균+분산*노이즈에러)x + (bias)

8. Rainbow

• 구글 딥마인드 → 7가지를 모두 합친 버전 DQN의 끝판왕

DQN [NIPS 2013], [Nature 2015] • Double DQN [AAAI 2016] • Prioritized Experience Replay [ICLR 2016] • Dueling Network Architecture [ICML 2016] • Multi-Step Learning [ICML 2016] • Distributional Reinforcement Learning [ICML 2017] • Noisy Nets [ICLR 2018]

References

David Silver